Considere uma onda transversal que se propaga no eixo e é dada pela equação
.
O gráfico abaixo apresenta o instantâneo do deslocamento (em ) em função da posição (em ) no instante . Já o gráfico apresenta o deslocamento (em ) em função do tempo (em ) para . Expressando suas respostas no sistema internacional de unidades (SI), determine:
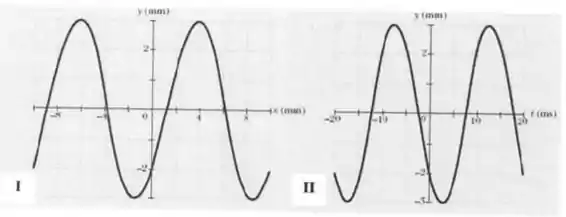
- A amplitude e o número de onda .
- O período e a frequência angular .
- A constante de fase .
Passo 1
Lembrando que a amplitude é dada pela distância do eixo até o ponto máximo da curva e é o tamanho de um comprimento de onda.
Pela leitura do gráfico :
Passo 2
Lembrando que o período () é a distância entre duas cristas. Pelo gráfico , vemos que:
Passo 3
Como :
Passo 4
Sabemos que:
Mas para e , temos:
Assim:
Resposta
- e
- e
Exercícios de Livros Relacionados
13.1. A corda de um piano emite um lá médio vibrando com uma frequência primaria igual a 220 Hz. a) Calcule o período e a frequência angular. b) Calcule a frequência angular de uma soprano emitindo um
Feixes de laser enviados para a Lua são um recurso rotineiro para se determinar com precisão a distância entre a Terra e a Lua. No entanto, para determinar a distancia com precisão, correções devem se
Use a equação de onda para determinar a velocidade de uma onda dada por y x , t = 3,00m m sen [ 4,00m - 1 x - 7,00s - 1 t ] .
Se, no exemplo 15.3 você não desprezasse a massa da corda, qual seria a velocidade da ondaNa extremidade inferior da corda;No meio da corda;Na extremidade superior da corda?
Um oscilador harmônico simples em x = 0 gera uma onda em uma corda. O oscilador opera em uma frequência de 40 H z e com uma amplitude de 3 c m . A corda possui uma densidade linear de 50 g / c m e est