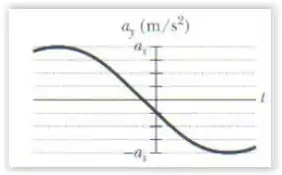
A figura abaixo mostra a aceleração transversal em função do tempo do ponto de uma corda, quando uma onda com a forma geral passa pelo ponto. A escala do eixo vertical é definida por . Qual é o valor de ?
Passo 1
Sendo:
Podemos dizer que:
Derivando mais uma vez para acharmos a aceleração transversal chegamos a:
Passo 2
Como :
Já que seno varia de até :
=
Pelo gráfico da figura, .
Passo 3
Pelo gráfico podemos ver também que quando , .
Logo:
ou
ou
Passo 4
Pra saber qual o valor correto da constante de fase, podemos fazer:
Como essa derivada acima é igual a inclinação da tangente na curva, no ponto , temos que a curva é decrescente, logo:
Assim:
É importante lembrar que quando acrescentamos , sendo n qualquer número inteiro, o ângulo também é válido como resposta.
Resposta
Exercícios de Livros Relacionados
13.1. A corda de um piano emite um lá médio vibrando com uma frequência primaria igual a 220 Hz. a) Calcule o período e a frequência angular. b) Calcule a frequência angular de uma soprano emitindo um
Feixes de laser enviados para a Lua são um recurso rotineiro para se determinar com precisão a distância entre a Terra e a Lua. No entanto, para determinar a distancia com precisão, correções devem se
Use a equação de onda para determinar a velocidade de uma onda dada por y x , t = 3,00m m sen [ 4,00m - 1 x - 7,00s - 1 t ] .
Se, no exemplo 15.3 você não desprezasse a massa da corda, qual seria a velocidade da ondaNa extremidade inferior da corda;No meio da corda;Na extremidade superior da corda?
Um oscilador harmônico simples em x = 0 gera uma onda em uma corda. O oscilador opera em uma frequência de 40 H z e com uma amplitude de 3 c m . A corda possui uma densidade linear de 50 g / c m e est