UFF, Cálculo 2B, Listas GMA, Lista 1, questão 3.
Descreva e esboce o maior domínio possível da função real de duas variáveis, isto é, descreva analiticamente e represente geometricamente o maior subconjunto do que torna a expressão que define a função verdadeira em .
Passo 1
Vamos lá, temos uma raiz. A primeira coisa que fazemos quando temos uma raiz é dizer que o que está dentro dela tem que ser maior ou igual que zero.
Beleza, agora temos uma inequação modular.
Mas tranquilo, isso não é nada demais. Então, resolvendo para , pelas propriedades da inequação modular, temos:
Poderíamos fazer para também. Ai seria:
ou
Passo 2
Mas, para esboçar esse domínio, vamos ficar com
Só porque a gente tá mais acostumado a ter o escrito em função de .
Assim, desenhando o gráfico de
E
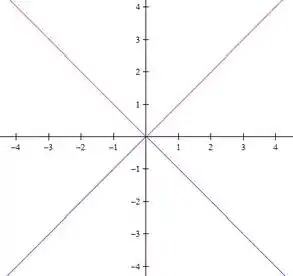
Nossa expressão do domínio diz que o deve estar entre esses dois gráficos. Assim, o domínio da nossa função são esses dois triângulos entre o gráfico vermelho () e azul ().
Resposta
