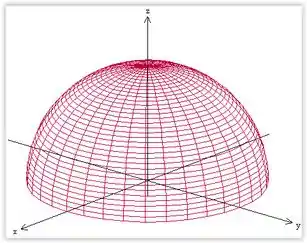
Esboce o gráfico da função
Passo 1
Identificar a superfície:
Fazer :
Essa é a equação da esfera!
Passo 2
Mas como
Devemos ter . Portanto, é apenas a parte superior da esfera.
Além disso, como estão elevados ao quadrado serão sempre positivos. Com aquele sinal de menos ali na frente eles vão sempre ser quantidades que vão subtrair! Portanto, o máximo ocorre onde . Ou seja, :
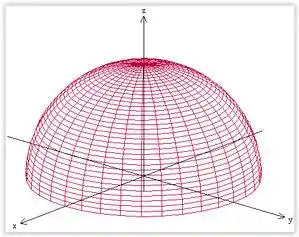
Resposta
Exercícios de Livros Relacionados
Seja g x , y = c o s ( x + 2 y ) .Calcule g ( 2 , - 1 ) .Determine o domínio de g . Determine a imagem de g
Seja f x , y , z = x + y + z + ln ( 4 - x 2 - y 2 - z 2 ) .Calcule f ( 1,1 , 1 ) .Determine o domínio de f .
Seja f x , y =x 2 e 3 x y .(a) Calcule f 2,0 .(b) Determine o domínio de f .(c) Determine a imagem de f .
As alturas de onda h em mar aberto dependem da velocidade v do vento e do tempo t que o vento tem soprado a essa velocidade. Os valores da função h = f v , t , td estão registrados nos pés na Tabela 4
1. Desenhe a imagem:c)F (t) = (t , t , 1) , t = 0