Curvas Parametrizadas, Funções de Várias Variáveis
Sejam e , . Sabendo que a imagem de está contida no gráfico de , encontre . Esboce .
Passo 1
Se a imagem de está sobre o gráfico de , então podemos substituir pela primeira coordenada de e pela segunda, tendo:
Beleza? Só o que fizemos foi parametrizar com ;)
Passo 2
Essa parametrização que encontramos nada mais é do que a função que a terceira coordenada dos os pontos da curva obedecem! Assim, a curva é:
E agora, o que faremos? Vamos encontrar uma relação entre e , e ver se ela é uma curva plana, uma espiral, ou o que quer que seja! Temos que:
Somando as duas coordenadas, temos:
Beleza, e isso nos diz que, no plano , a projeção da curva é uma reta! E, neste caso, a curva está sobre o plano !
Passo 3
Vamos esboçar a superfície para visualizar melhor o que está se passando e ver quem realmente é a curva ? Temos:
Se fizermos , veremos, nesse plano, a seguinte curva:
Ou seja, uma parábola deslocada em no sentido positivo do eixo e em no sentido positivo do eixo !
Se fizermos , veremos, nesse plano, a seguinte curva:
Ou seja, uma parábola deslocada em no sentido positivo do eixo e em no sentido positivo do eixo !
Percebe? Temos um paraboloide, que não está centrado na origem, mas em , e deslocado em no eixo . Se cortarmos esse paraboloide pelo plano , teremos:
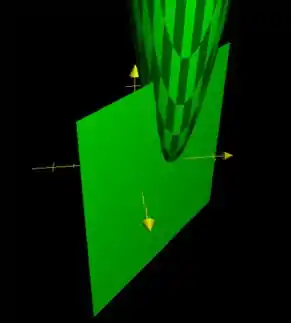
Uma parábola!
Resposta
a) A curva é e é uma parábola.