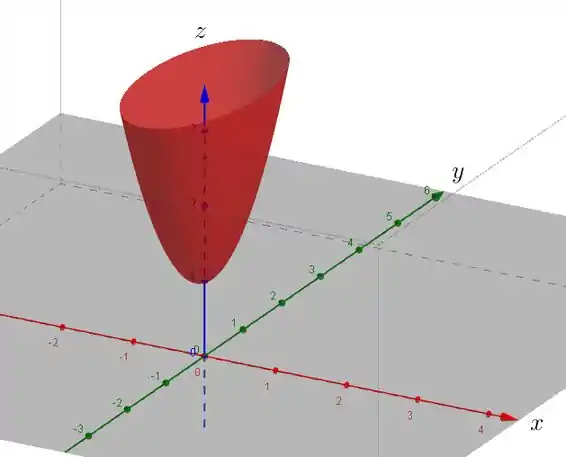
Esboce o gráfico da função
Passo 1
Temos uma função de variáveis, então vamos escrevê-la na forma
Essa é a equação da superfície que temos que esboçar.
Prestando atenção, podemos ver que ser trata da equação de um paraboloide. Dá até pra reparar que ele é voltado pra cima, porque os coeficientes multiplicando e são positivos.
Vamos ver isso com calma analisando as interseções do gráfico com os planos coordenados :)
Passo 2
Então vamos anular as variáveis, uma por uma.
Começando pela variável por exemplo, podemos ver como é a interseção da superfície com o plano . Fazendo :
Opa! Uma equação de uma parábola, bem tranquila! Saca só:
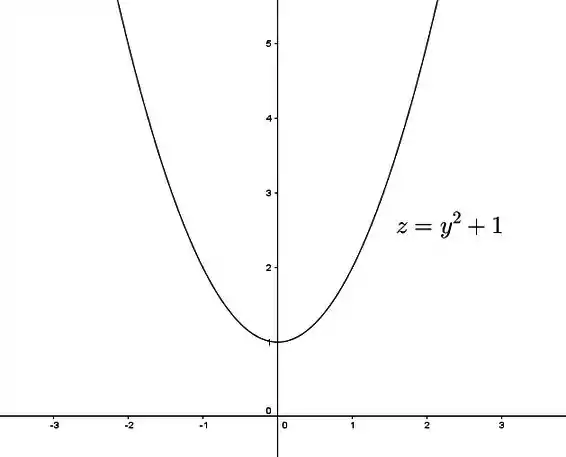
Passo 3
Agora vamos zerar a variável ! Assim, no plano vamos ter:
que também é uma parábola tranquila de esboçar. Ela vai ser bem parecida com a outra, mas por causa desse ela vai ser mais “pontuda”:
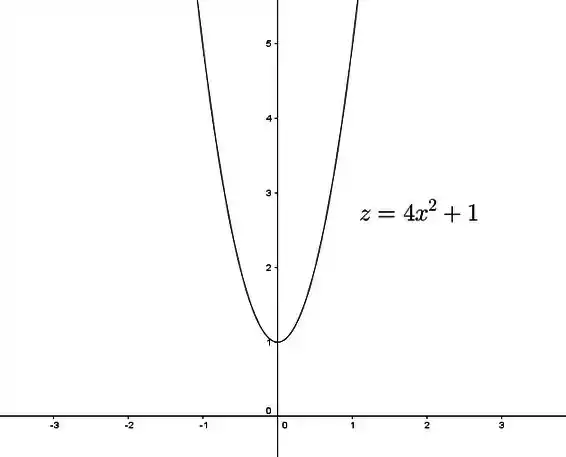
Passo 4
Agora só falta zerar a variável !
Fazendo, portanto, , obtemos:
Repare que essa equação não tem solução!!
Temos
Ou seja, a nossa superfície fica acima do plano !
Passo 5
Resumindo, o nosso gráfico é um paraboloide elíptico voltado pra cima, com vértice no ponto . Ele é mais largo no plano e mais magrinho no plano .
Agora, tendo em mente tudo isso que vimos, eu só te digo uma coisa: partiu esboçar essa bagaça!!
O gráfico ficaria assim:
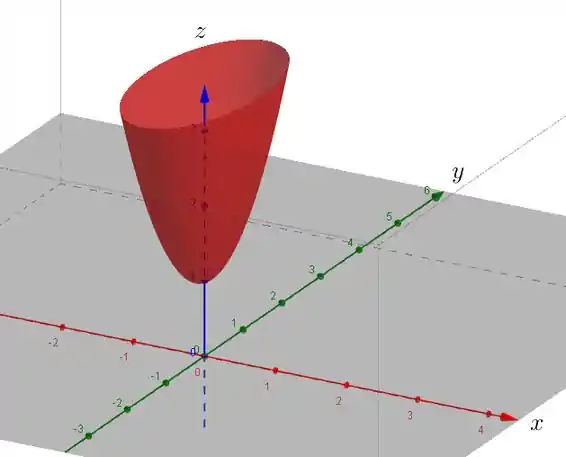
Resposta