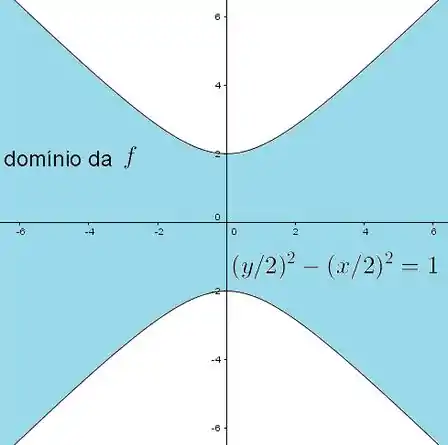
Seja . Determine e represente o domínio máximo da função .
Passo 1
A única restrição da função é a raiz quadrada. Devemos ter:
Dividindo tudo por :
Passo 2
Portanto, o domínio da função é a região , que é a região do plano entre as componentes da hipérbole .
Ele nem pediu pra esboçar mas saca só como é o domínio:
Resposta
Exercícios de Livros Relacionados
Seja g x , y = c o s ( x + 2 y ) .Calcule g ( 2 , - 1 ) .Determine o domínio de g . Determine a imagem de g
Seja f x , y , z = x + y + z + ln ( 4 - x 2 - y 2 - z 2 ) .Calcule f ( 1,1 , 1 ) .Determine o domínio de f .
Seja f x , y =x 2 e 3 x y .(a) Calcule f 2,0 .(b) Determine o domínio de f .(c) Determine a imagem de f .
As alturas de onda h em mar aberto dependem da velocidade v do vento e do tempo t que o vento tem soprado a essa velocidade. Os valores da função h = f v , t , td estão registrados nos pés na Tabela 4
1. Desenhe a imagem:c)F (t) = (t , t , 1) , t = 0