Encontre o domínio da função
Passo 1
Temos uma questão que pede pra gente descobrir onde a função existe (ou seja, qual é o seu domínio). Mas, convenhamos... é muito mais fácil descobrir onde ela não existe!!
Nossa função é uma fração, então a primeira coisa que devemos bater o olho é no denominador: ele não pode valer 0.
Vamos ver como é o gráfico da função logaritmo:
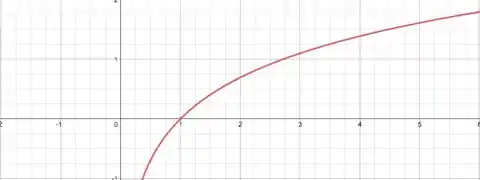
Olha só! Quando seu argumento é , seu valor é (é o ponto onde ela corta o eixo x). Portanto, como o valor do denominador da função do enunciado não pode valer ,
Igualando um argumento ao outro...
Passo 2
Ainda olhando para o gráfico da função logaritmo, observe que ela não está definida em ou números menores que 0. Ou seja, o argumento da função logaritmo só podem ser números maiores do que :
Passo 3
Pronto, agora que todos os problemas do denominador foram devidamente resolvidos, podemos olhar pra parte de cima da fração
Veja, temos aqui uma raíz quadrada
E seu interior não poder valer menos do que
Assim, fica:
Passo 4
Agora é só juntar tudo!
Do passo temos que
Do passo 2 temos que
E, do passo 3, temos que
Assim, nosso domínio é definido por:
Se não se sentir à vontade com a notação matemática (como eu... rsrs), é só escrever por extenso mesmo na prova! Isso aí em cima, lendo em português, diz que o domínio da função é o conjunto dos pontos , sendo e pertencendo aos reais, tais que e