Determine e esboce o domínio de
Passo 1
Essa é tranquila! O comando está bem claro, então é só colocar os nossos passos em ação!
Vendo a nossa função com atenção, podemos destacar dois casos que interferem no domínio:
1-Dentro das raízes de índice par não pode ter número menor que
2-O denominador da fração não pode ser
Agora podemos estabelecer as restrições da função!
Passo 2
A primeira restrição é dentro das raízes pares não pode ter número menor que .
Então, vamos analisar o termo,
Para que dentro da raiz seja maior ou igual a zero, temos que
Também temos na função outra raíz par,
Para que dentro da raiz seja maior ou igual a zero, temos que
Por último, também temos um termo que é uma raiz impar,
Como é uma raíz ímpar, não temos restrição nenhuma!
Passo 3
A segunda restrição é que o denominador da fração não pode ser
Então vamos analisar o termo que é uma fração
Para que o denominador não seja zero, temos que
Logo,
Agora, unindo as duas restrições para este termo, temos que , o argumento da raíz, não pode ser menor que ! Então vamos atualizar o resultado que encontramos no Passo 2.
Então a restrição fica assim,
Passo 4
Então agora chegamos em duas condições para se avaliar. A primeira é,
E como que você descobre o que essa desigualdade representa no plano? Basta fingir que é uma igualdade!
Veja, ficaria assim:
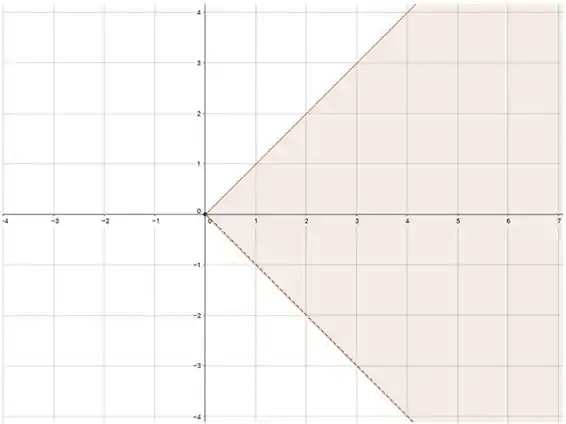
Essa é a reta que aponta pra baixo, passando pelo segundo e quarto quadrantes! Agora é só colocar o sinal da desigualdade de novo!
Ou seja, essa parte do domínio é tudo à direita da reta , excluindo a reta (porque o sinal é só de “maior que”, e nao de “maior ou igual”). Enfim, encontramos isso:
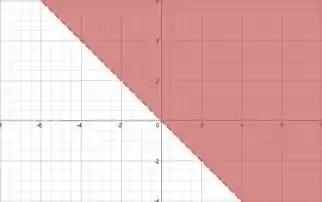
A outra condição é
temos algo parecido. Agora teremos a reta , e como o sinal é de maior ou igual, a reta está inclusa, é pegamos tudo à sua direita. Fica assim:
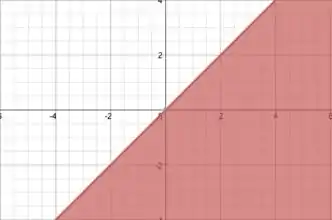
Passo 5
Pra gente esboçar o domínio todo é só sobrepor os que já temos! Fica assim:

Resposta
O domínio é dado por que é a interseção do gráfico acima
E seu esboço é: