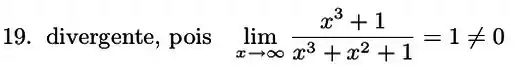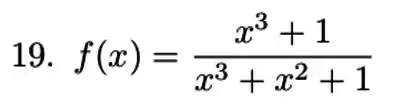
Passo 1
Precisamos determinar a convergência de
Perceba que um termo no denominador, que faz com que tendendo ao infinito essa função deva tender para . No entanto, se aplicarmos o limite com .
Aplicando l’Hopital
O limite da função não é 0. Então nossa função diverge, fazendo com que a integral também seja divergente.
Resposta
Exercícios de Livros Relacionados
Calcule:int_1^(+ oo) (1)/(sqrt(x)) d x
Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ 2 π ∞ s e nxd x
Se f t é contínua para t ≥ 0 , a Transformada de Laplace de f é a função F definida por F s = ∫ 0 ∞ f t e - s t d t e o domínio de F é conjunto de todos os números s para os quais a integral converge.
Se f t é contínua para t ≥ 0 , a Transformada de Laplace de f é a função F definida por F s = ∫ 0 ∞ f t e - s t d t e o domínio de F é conjunto de todos os números s para os quais a integral converge.
Estime o valor numérico de ∫ 0 ∞ e - x 2 d x escrevendo a integral como uma soma de ∫ 0 4 e - x 2 d x e ∫ 4 ∞ e - x 2 d x . Aproxime a primeira integral usando a Regra de Simpson com n = 8 e mostre qu