Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Impróprias – Limites Sendo Infinito

Ver Teoria
Exercício 621234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606163646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

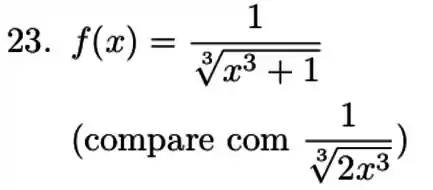
Passo 1

Nesse exercício, temos que determinar a convergência da integral imprópria

∫ 1 ∞ 1 x 3 + 1 3 d x

Para isso, o enunciado recomenda que façamos a comparação com

1 2 x 3 3

Passo 2

Então vamos lá! Nossos limites estão entre 1 e ∞ . Então

x ≥ 1 > 0

Para esses valores de x sempre teremos

1 x 3 + 1 3 ≥ 1 2 x 3 3 > 0

Se aplicarmos a integral nessa expressão

∫ 1 ∞ 1 x 3 + 1 3 d x ≥ ∫ 1 ∞ 1 2 x 3 3 d x > 0

Passo 3

Vamos analisar então a convergência de

∫ 1 ∞ 1 2 x 3 3 d x

Para isso, precisamos aplicar o limite

∫ 1 ∞ 1 2 x 3 3 d x = lim a → ∞ ⁡ ∫ 1 a 1 2 x 3 3 d x

E resolver normalmente a integral

∫ 1 a 1 2 x 3 3 d x

∫ 1 a 1 2 x 3 3 d x = 1 2 3 ∫ 1 a d x x

= 1 2 3 ln ⁡ x 1 a

Aplicando os limites de integração

∫ 1 a 1 2 x 3 3 d x = 1 2 3 ln ⁡ a - 1 2 3 ln ⁡ 1

∫ 1 a 1 2 x 3 3 d x = 1 2 3 ln ⁡ a

Voltando para o limite

∫ 1 ∞ 1 2 x 3 3 d x = lim a → ∞ ⁡ ∫ 1 a 1 2 x 3 3 d x

∫ 1 ∞ 1 2 x 3 3 d x = lim a → ∞ ⁡ 1 2 3 ln ⁡ a

∫ 1 ∞ 1 2 x 3 3 d x = ∞

Passo 4

Mas lá no passo 2 tínhamos chegado à conclusão de que

∫ 1 ∞ 1 x 3 + 1 3 d x ≥ ∫ 1 ∞ 1 2 x 3 3 d x > 0

E isso não é possível se

∫ 1 ∞ 1 2 x 3 3 d x = ∞

Logo, a integral diverge.

Resposta

Exercícios de Livros Relacionados

Calcule:int_1^(+ oo) (1)/(sqrt(x)) d x
Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ 2 π ∞ s e nxd x
Se f t é contínua para t ≥ 0 , a Transformada de Laplace de f é a função F definida por F s = ∫ 0 ∞ f t e - s t d t e o domínio de F é conjunto de todos os números s para os quais a integral converge.
Se f t é contínua para t ≥ 0 , a Transformada de Laplace de f é a função F definida por F s = ∫ 0 ∞ f t e - s t d t e o domínio de F é conjunto de todos os números s para os quais a integral converge.
Estime o valor numérico de ∫ 0 ∞ e - x 2 d x escrevendo a integral como uma soma de ∫ 0 4 e - x 2 d x e ∫ 4 ∞ e - x 2 d x . Aproxime a primeira integral usando a Regra de Simpson com n = 8 e mostre qu