Nos exercícios a discuta a convergência da integral para a função dada.
Passo 1
Cara, primeiro percebe o seguinte: se uma função é infinita num intervalo, a sua integral naquele intervalo também será infinita, já que a integral é um somatório de valores daquela função (ou você pode pensar como área debaixo da função e acima do eixo ).
No nosso caso, é infinita entre e . Dá uma olhada aqui no gráfico:
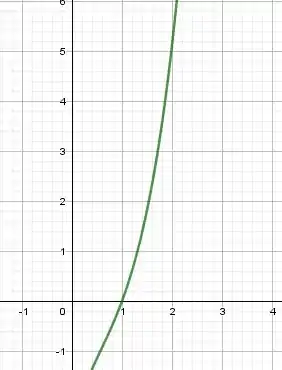
Tá vendo só? A partir do , ela só cresce, então essa integral será infinita.
Vamos provar isso matematicamente. Para isso, basta a gente calcular o limite dessa função para quando e ver se ele realmente vai pra infinito.
Resposta
divergente, pois .
Exercícios de Livros Relacionados
Calcule:int_1^(+ oo) (1)/(sqrt(x)) d x
Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ 2 π ∞ s e nxd x
Se f t é contínua para t ≥ 0 , a Transformada de Laplace de f é a função F definida por F s = ∫ 0 ∞ f t e - s t d t e o domínio de F é conjunto de todos os números s para os quais a integral converge.
Se f t é contínua para t ≥ 0 , a Transformada de Laplace de f é a função F definida por F s = ∫ 0 ∞ f t e - s t d t e o domínio de F é conjunto de todos os números s para os quais a integral converge.
Estime o valor numérico de ∫ 0 ∞ e - x 2 d x escrevendo a integral como uma soma de ∫ 0 4 e - x 2 d x e ∫ 4 ∞ e - x 2 d x . Aproxime a primeira integral usando a Regra de Simpson com n = 8 e mostre qu