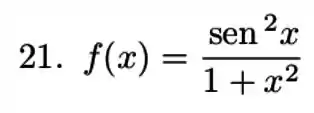
Passo 1
Nesse exercício, temos que determinar a convergência da integral imprópria
Mas essa integral não é trivial de ser resolvida e apenas precisamos determinar apenas a convergência, então vamos fazer isso pelo método da comparação.
Passo 2
Bom, vamos observar que
Então, se aplicarmos a integral
Passo 3
Vamos analisar então a convergência de
Para isso, precisamos aplicar o limite
E resolver normalmente a integral
Essa é uma daquelas integrais trigonométricas
Aplicando os limites de integração
Voltando para o limite
Sabemos que
Então
Passo 4
Bom, então se
E
Então nossa integral é convergente.
Resposta
Exercícios de Livros Relacionados
Calcule:int_1^(+ oo) (1)/(sqrt(x)) d x
Determine se cada integral é convergente ou divergente. Calcule aquelas que são convergentes. ∫ 2 π ∞ s e nxd x
Se f t é contínua para t ≥ 0 , a Transformada de Laplace de f é a função F definida por F s = ∫ 0 ∞ f t e - s t d t e o domínio de F é conjunto de todos os números s para os quais a integral converge.
Se f t é contínua para t ≥ 0 , a Transformada de Laplace de f é a função F definida por F s = ∫ 0 ∞ f t e - s t d t e o domínio de F é conjunto de todos os números s para os quais a integral converge.
Estime o valor numérico de ∫ 0 ∞ e - x 2 d x escrevendo a integral como uma soma de ∫ 0 4 e - x 2 d x e ∫ 4 ∞ e - x 2 d x . Aproxime a primeira integral usando a Regra de Simpson com n = 8 e mostre qu