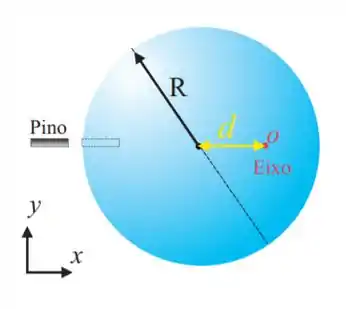
15. Um disco homogêneo de raio e massa está fixo por um pino a uma parede vertical no plano , conforme a figura abaixo. O disco pode girar, sem atrito, ao redor do eixo fixo que é perpendicular ao plano , e que passa pelo ponto O distante do centro do disco. O disco não encosta na parede e, portanto, não há atrito com a parede vertical. Inicialmente, o centro de massa está na altura do eixo de rotação e um pequeno pino impede o disco de girar. O módulo do vetor aceleração angular do disco no instante em que o pino é removido, em , é:

Passo 1
E aí galerinha! Olha nós aqui de novo!
Novamente temos uma questãozinha de um disco girando em torno de um eixo conectado ao pino!
Por isso, sem mais delongas! Já sabe, né!?
Vamos fazer o diagrama de corpo livre desse danado pra ver o que a gente pode fazer.
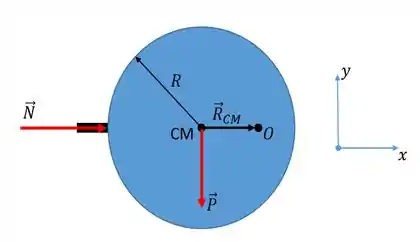
Temos duas forças agindo sobre o nosso disco, que são a força peso (uma vez que ele tem massa) e a força normal que o pino exerce sobre o disco.
Repara que a gente até fez um sistema de coordenadas ali no esboço... Tudo pra facilitar o entendimento, hein!?
Agora se liga! é o ponto por onde passa o eixo ao redor do qual o disco gira. É o ponto por mais importante, junto com o centro de massa, aqui pra nossa análise. Sabe por quê?
Ora bolas! Olha de novo a figura que fizemos! Presta atenção na localização da força peso! A força responsável pelo torque no eixo fazendo com que o disco gire é a força peso, que age no seu centro de massa. Sendo assim, pela imagem temos que:
Onde é o vetor posição, no caso a distância , que indica o ponto de aplicação da força peso, (no centro do disco) em relação ao ponto e o símbolo indica o produto vetorial entre os vetores e a força peso .
E lá da geometria analítica, sabemos que para calcular o módulo do torque, basta fazer:
Como os vetores e são perpendiculares então:
Passo 2
Continuando nosso raciocínio, já sabemos que se um torque está sendo gerado no eixo ao longo do disco, então ele vai começar a girar, não é mesmo!? Ele começa a girar, adquirindo uma aceleração angular . Além disso, como nosso disco tem massa, e por conseguinte momento de inércia , em uma rotação de corpo rígido, temos que:
Tirando o módulo, ou seja, deixando em valor absoluto:
Passo 3
A próxima coisa a se fazer é determinar o momento de inércia do disco. Pois bem! Pelo teorema dos eixos paralelos:
Uma vez que o momento de inércia passando pelo centro de massa de um disco é:
Olhando a última figura do , chegamos ao seguinte valor para :
Assim, o módulo da aceleração angular vai ser igual à:
Substituindo os valores numéricos dados no enunciado:
Conseguimos chegar ao nosso resultado!
Bora pra próxima!
Tamo quase acabando!