Um fio ideal se encontra enrolado em torno de um cilindro maciço de massa e raio e não desliza sobre o cilindro. O cilindro gira com atrito desprezível em torno de um eixo horizontal fixo, sendo seu momento de inércia em relação a esse eixo. O fio passa por uma polia de massa desprezível. A outra extremidade do fio está amarrada a uma bola de borracha de massa , de raio desprezível, que se encontra inicialmente em repouso a uma altura do solo, como mostra a figura.
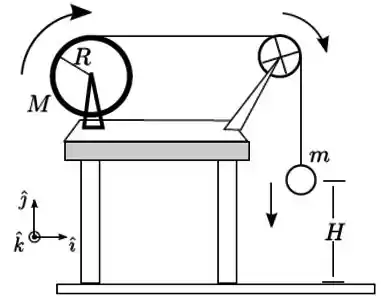
Considere que: os fios são ideais; os fios permanecem esticados durante todo o tempo; a resistência do ar é desprezível; a gravidade tem módulo conhecido.
Supondo que o fio se encontre inicialmente esticado e a bola colida elasticamente com o solo, determine:
a) o módulo da velocidade com que a bola colide com o solo;
b) o módulo da tensão no fio no instante imediatamente anterior à colisão da bola;
Passo 1
a)
Vamos considerar o sistema cilindro+polia+bola. Mas como a massa da polia é desprezível, na prática vai ser o sistema cilindro+bola.
Os atritos são desprezíveis, então podemos aplicar a conservação da energia mecânica!
sendo a energia mecânica inicial e a energia mecânica no momento da colisão com o solo.
Passo 2
Inicialmente, a bola está em repouso, então a energia mecânica do sistema é igual à energia potencial gravitacional da bola:
Obs: não vamos considerar a energia potencial gravitacional do cilindro porque ele fica parado na mesma altura, então não serviria pra nada. Se a gente acrescentar essa energia na e na poderíamos simplesmente cortá-la dos 2 lados depois.
Passo 3
Já na hora da colisão, temos que considerar não só a energia cinética de translação da bola, mas também a energia cinética de rotação do cilindro:
sendo o momento de inércia do cilindro.
Passo 4
Também temos a relação
Então vamos ter
Passo 5
Então a energia mecânica do sistema no instante da colisão é:
Passo 6
Show! Então a equação de conservação da energia é:
Passo 7
Vamos simplificar a fração do lado direito multiplicando por 4, no numerador e no denominador:
Passo 8
b)
As forças atuando na bola são a tensão do fio (a qual queremos achar o módulo), apontando pra cima, e o próprio peso da bola, apontando pra baixo:

Passo 9
Então, pela 2ª lei de Newton, na bola:
sendo a aceleração da bola.
Como a bola está descendo, em módulo a equação vai ser:
E substituindo , isso dá:
Passo 10
Agora vamos dar uma olhada no cilindro.
As forças agindo nele são seu peso e a tensão do fio :
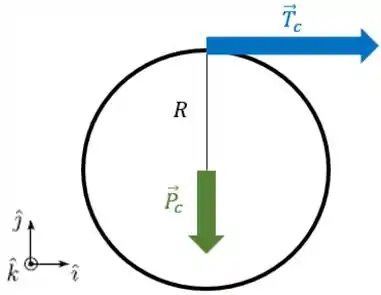
Passo 11
Como a força peso age diretamente no centro do cilindro, onde passa o eixo de rotação, ela não realiza torque em relação a esse eixo: só a tensão faz torque!
Então o torque resultante agindo no cilindro é igual ao torque da tensão:
Passo 12
O torque realizado pela força de tensão no fio é:
E como os fios são ideais, essa tensão tem o mesmo módulo da tensão que age na bola!
Ou seja,
Passo 13
E, pela versão pra rotação da 2ª lei de Newton,
Ou seja,
O que, em módulo, dá:
Passo 14
Vamos substituir :
Passo 15
E antes a gente achou:
Ou seja,
Passo 16
A única variável que a gente não conhece aí é a , então vamos isolá-la:
Passo 17
Show! Agora vamos substituir essa na equação
o que dá:
Esse é o módulo da tensão no fio logo antes da colisão! Mas tá meio feio, então podemos multiplicar em cima e em baixo por :
Resposta
a)
b)