No disco de e de raio são aplicadas as forças como indicadas na figura. O disco pode girar e torno do eixo que passa pelo ponto e é perpendicular ao disco.
Dados: ; ;
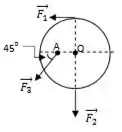
- Calcule o torque resultante em relação ao eixo de rotação que passa em .
- Calcule o momento de inércia do disco em relação ao eixo de rotação que passa em .
- Calcule a aceletação angular do disco e a aceleração tangencial no ponto onde a força atua.
Passo 1
Lembra-se de torque, correto?
Então, o toque total é a soma de cada toquezinho no ponto.
Vamos começar pelo mais fácil
Isso porque a força aponta exatamente sobre o eixo de rotação e o ângulo entre e é zero!
O torque exercido pela força 1 é isso aqui
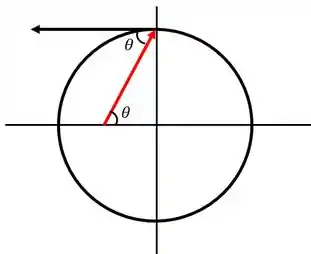
Agora a gente tem que procurar o seno desse ângulo . Tá vendo que tem um triângulo retângulo ali?! A hipotenusa é e o cateto oposto é o raio do círculo!
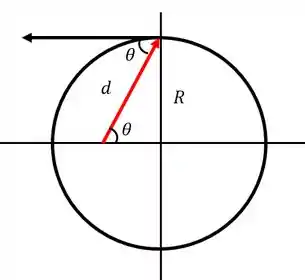
Então:
Jogando na equação do torque
Assim:
A mesma coisa vai acontecer pra força 2!
Agora as dúvidas: por que o torque da é negativo? Porque o torque devido a esta força ocorre no sentido horário
Com isso, temos que o torque total é:
Passo 2
Como o ponto não é o centro de massa do disco, teremos que usar o teorema dos eixos paralelos.
Momento de inércia em relação ao centro de massa para um disco:
Então temos:
Com o teorema dos eixos paralelos:
Passo 3
Como vimos na teoria,
Vamos aproveitar que já calculamos o torque resultante e o momento de inércia em , e vamos aplicar esta fórmula com estes valores.
Agora basta calcular a aceleração angular pela distância até o ponto que queremos estudar: