Um carretel é composto por um cilindro interno de raio e massa , enrolado por um fio ideal, com 2 discos idênticos, de massa e raio cada um, por fora do cilindro interno, concêntricos a este último (como um iô-iô). Inicialmente o carretel está em repouso em uma superfície horizontal quando o fio enrolado ao cilindro interno começa a ser puxado na direção horizontal, conforme a figura, por uma força de módulo . Observa-se que o cilindro rola sem
deslizar sobre a superfície horizontal e sabe-se que o momento de inércia de um cilindro de massa m e raio r′ em relação a um eixo que passa por seu eixo desimetria é .
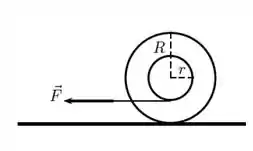
Indique as respostas em termos de .
(a) Mostre que o momento de inércia do carretel, em relação a seu eixo de simetria, vale
(b) Qual a direção e o sentido da força de atrito que atua no carretel?
(c) Determine o módulo e o sentido da aceleração do centro de massa do carretel.
(d) Qual a velocidade angular de rotação do carretel, em torno do eixo de simetria
que passa por seu centro de massa, após ele completar uma volta depois do instante
em que a força começa a atuar?
(e) Determine a energia cinética associada ao carretel no instante em que ele completa
a primeira volta após o início da aplicação da força .
Passo 1
Calcularemos o valor do momento de inércia do carretel.
Como o carretal é composto por 2 cilindros de raio e um cilindro de raio (todos com a mesma massa, podemos calcular seu momento de inércia da seguinte forma.
Passo 2
Responderemos a letra (b).
Como o cilindro rola sem deslizar sobre a superfície, podemos afirmar que existe o atrito. A força está sendo aplicada para a esquerda. Esta força ainda gera um momento no sentido horário. Para que haja o equilíbrio, o atrito deve compensar esta força, apontando para o lado oposto de . Logo, a força de atrito atua para a direita.
Passo 3
Calcularemos o módulo e o sentido da aceleração do centro de massa do carretel.
Fazendo o equilíbrio das forças, utilizando a segunda Lei de Newton, teremos:
Eixo y (considerando o eixo positivo para cima):
Eixo x (considerando o eixo positivo para a esquerda):
Utilizando a lei de Newton para a rotação, teremos:
Onde é o momento de inércia do corpo e é a aceleração angular. Para a condição sem deslizamento, pode ser calculado como:
Utilizando a fórmula da rotação (considerando a rotação anti-horária positiva), teremos:
Substituindo o valor de calculado na letra (a), teremos:
Simplificando dos dois lados da expressão, teremos:
Somando as equações :
Como o valor encontrado para a aceleração foi positivo, a aceleração aponta para a esquerda.
Passo 4
Calcularemos a velocidade angular após uma volta do carretel.
Como o movimento acontece sem deslizamento, podemos considerar que:
Como o movimento possui aceleração angular, podemos utilizar a fórmula do Torricelli para a rotação:
Como a velocidade angular inicial é nula e deseja-se saber a velocidade após uma volta , teremos:
Logo,
Passo 5
Calcularemos a energia cinética após uma volta do carretel.
No cálculo da energia cinética do cilindro, teremos uma parcela relacionada à tranlação e outra relacionada à rotação do conjunto.
A parcela relacionada à translação leva em consideração a velocidade do centro de massa .
Lembrando que , podemos calcular a energia cinética .
Logo,
Substituindo o valor de encontrado no item anterior, temos:
Resposta
A força de atrito atua para a direita.