Uma pequena esfera ligada a uma haste rígida leve gira em torno de um eixo perpendicular que está fixado à outra extremidade da haste. Em um certo sistema de referências, a sua velocidade angular é negativa, e a sua aceleração angular é positiva. Se um observador neste sistema de referências se posicionar de modo a ter o eixo de rotação apontando diretamente para si, ele observará a esfera:
- Girando no sentido horário e desacelerando.
- Girando no sentido anti-horário e desacelerando.
- Girando no sentido horário e acelerando.
- Girando no sentido anti-horário e acelerando.
- Primeiro girando no sentido anti-horário e, em seguida, no sentido horário.
Passo 1
Bom galera, o macete principal aqui é definir um eixo que seja perpendicular ao plano de rotação da esfera e que aponte da esfera pra cima. Como assim? Dessa forma:

Beleza? E esse eixo é o nosso sistema de referencia. Assim, pra que um vetor que represente a velocidade angular seja positivo nesse sistema, deve apontar na direção dele, se for negativo, na direção contrária. O mesmo vale pra aceleração.
Passo 2
Então, segundo o enunciado, os vetores devem estar assim:
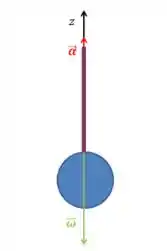
Beleza?
Agora, vamos olhar pra essa cena como se tivéssemos ali na pontinha do . Usando a regra da mão direita, vamos determinar o sentido de giração de cada vetor.
Passo 3
Então, olhando de cima:
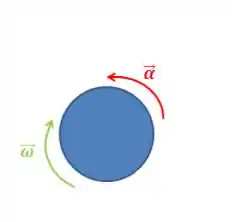
Cheque com a mão direita. Você vai ver que o vetor vai estar saltando pra fora da pagina e o vetor vai estar voltado para dentro da pagina.
Beleza?
Então:
A velocidade anular esta indo no sentido horário e desacelerando, já que a aceleração o faz girar no sentido contrário:
a)
Resposta
a)