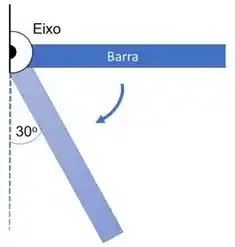
Uma barra de massa e comprimento roda livremente em um eixo localizado em uma de suas laterais. A barra é solta da posição horizontal. Qual a aceleração angular quando a barra faz um ângulo de 30º com a vertical. Considere que o momento de inércia de uma barra em torno do centro de massa é .
a)
b)
c)
d)
e)
Passo 1
Essa questão nos pede a aceleração angular da barra. Para encontrar essa aceleração angular, precisamos encontrar o torque resultante sobre ela, para isso, vamos dar uma olhada no diagrama do corpo livre dela:
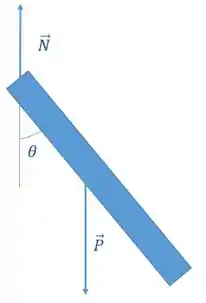
Beleza, vamos analisar então os torques em função do eixo de rotação dela. Olha aí, que essa normal não vai gerar torque, por que ela está bem em cima do eixo de rotação.
Mas cuidado agora, por que esse momento de inércia aí, tem que ser em relação ao eixo de rotação, e o momento de inércia dado é em relação do centro de massa da barra.
Passo 2
Calma, não se desespera.

Para encontrar o momento de inércia em relação ao eixo que passa em sua extremidade, é só fazer o Teorema dos Eixos Paralelos.
Passo 3
Agora é só correr pro abraço:
Resposta
Letra d)