Considere um pêndulo cônico formado por um fio ideal de comprimento e uma pequena esfera de massa que descreve um movimento circular uniforme de raio e velocidade angular , conforme a figura a seguir.
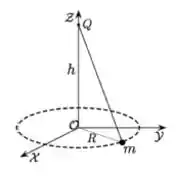
Sabemos que as quantidades relacionadas à rotação podem depender do ponto em relação ao qual são calculadas. Comparando sempre as quantidades em relação ao ponto O (centro do movimento circular) e Q (ponto onde o fio está fixo) qual a única das quantidades a seguir é a mesma?
(a) Torque causado pela força peso na esfera.
(b) Torque causado pela tração do fio na esfera.
(c) Torque causado pela força resultante na esfera.
(d) Momento angular da esfera.
Passo 1
Temos um pêndulo cônico e queremos comparar algumas quantidades com relação ao ponto O e ao ponto Q.
Dando uma olhada rápida nas alternativas, vemos que todas envolvem o torque de alguma força aplicada na partícula ou seu momento angular.
O torque é dado por:
Enquanto o momento angular de uma partícula é dado por:
Como essas grandezas dependem do vetor posição, já podemos desenhar o vetor posição a partir do ponto O e o vetor posição do ponto Q :
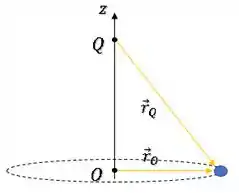
Agora vamos analisar cada grandeza.
Passo 2
(a) Torque causado pela força peso na esfera.
Vamos olhar para a força peso:
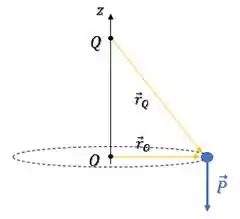
O torque da força peso para o ponto O é:
Como os vetores são perpendiculares, o módulo do torqe fica apenas o produto dos módulos e sua direção perpendicular ao plano que estamos observando:
Já o torque da força peso para o ponto Q é:
Bom, para calcular esse produto vetorial podemos pegar a componente de perpendicular ao vetor e multiplicar seu módulo pelo módulo da força. Além disso, a direção do torque também será perpendicular ao plano que estamos olhando:
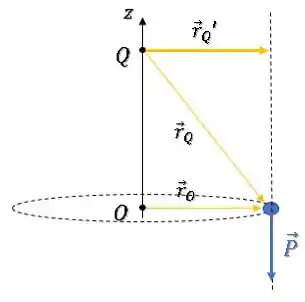
Repara que a componente é exatamente igual em módulo ao vetor , então:
Assim:
Logo, os torquess da força peso com relação ao ponto O e Q são iguais.
A letra (a) está correta.
Vamos passar rapidamente pelas outras e observar porque são diferentes.
Passo 3
(b) Torque causado pela tração do fio na esfera.
A força de tração está na direção do fio:
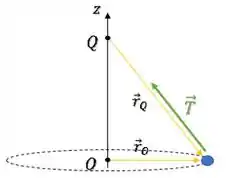
Como o vetor é paralelo ao vetor , o torque dessa força com relação ao ponto Q é nulo:
Enquanto isso, o torque da força com relação ao ponto O não será nulo:
Passo 4
(c) Torque causado pela força resultante na esfera.
Como a esfera realiza um movimento circular na base do “cone”, a força resultante atuando sobre ela é uma força centrípeta e aponta para o centro da trajetória circular:
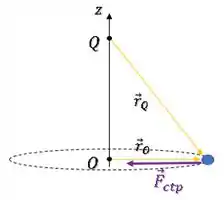
Assim, pela mesma lógica do item anterior, o torque da força resultante com relação ao ponto O será nulo pois os vetores são paralelos:
Enquanto o torque da força resultante com relação ao ponto Q não será nulo:
Passo 5
(d) Momento angular da esfera.
O momento angular é dado por:
Para ambos os vetores posição e , o vetor momento linear faz um ângulo de com eles.
Portanto, o módulo do momento angular em ambos os casos ficará o produto dos módulos dos vetores posição e momento linear :
Como o módulo do vetor posição é maior que o módulo de , os momentos angulares terão valores diferentes.
Além disso, os vetores momento linear para o ponto Q e para o ponto O estarão em direções diferentes.
Resposta
Letra (a)