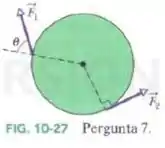
Na Fig. 10-27, duas forças e , agem sobre um disco em torno do centro como um carrossel. As forças mantêm os ângulos indicados durante a rotação, que ocorre no sentido anti-horário e com velocidade angular constante. Precisamos diminuir o ângulo de sem mudar o módulo de , (a) Para manter a velocidade angular constante, devemos aumentar, diminuir ou manter constante o módulo de ? (b) A força tende a girar o disco no sentido horário ou anti-horário? (c) E a força ?
Passo 1
O primeiro passo aqui é montar uma equação que deixe explícita todas as variáveis do problema. Nós acabamos de aprender uma:
Beleza, o é constante e o é uma variável que vamos analisar. Resta pra nós calcular o valor de , o torque resultante das forças que agem no corpo.
Passo 2
Sabemos que:
Pela definição de torque, temos que:
Pela regra da mão direita, conseguimos o sentido do vetor , que aponta para dentro da tela. Já o módulo, usamos que:
Usaremos que o eixo é orientado positivamente para fora da tela do computador, então:
Passo 3
Faremos o mesmo agora com a força :
Combinando os resultados da regra da mão direita com a fórmula simplificada para o módulo:
Passo 4
Combinando os resultados:
E então:
Na letra (a), se deseja manter a velocidade angular constante, ou seja, a aceleração angular deve ser zero.
Se precisamos manter o módulo de constante e diminuir o ângulo , perceberemos que o lado direito da equação acima irá diminuir. Portanto, para manter a equação válida devemos diminuir o módulo de .
Passo 5
Na letra (b), podemos imaginar o movimento no ponto onde a força está aplicada.
Sabendo que somente a componente perpendicular ao raio realizará esse movimento, podemos concluir que o disco giraria no sentido horário se somente a força fosse aplicada.
Já na letra (c), aplicando o mesmo conceito, , conseguimos concluir que o disco giraria no sentido anti-horário se somente a força fosse aplicada.
Resposta
- Diminuir
- Horário
- Anti-horário