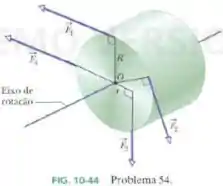
Na figura abaixo um cilindro com uma massa de pode girar em torno de seu eixo central, que passa pelo ponto . As forças mostradas têm os seguintes módulos: , , e . As distâncias radiais são e . Determine (a) o módulo e (b) a orientação da aceleração angular do cilindro. (Durante a rotação, as forças mantêm seus ângulos em relação ao cilindro.)
Passo 1
Esse é mais um exercício sem mistério, a abordagem é a mesma. Primeiramente, vamos encontrar o torque resultante das 4 forças e depois aplicar a relação:
Para então encontrar a aceleração angular.
Devemos lembrar também que essa relação também é válida na forma vetorial, ou seja:
O que significa que a rotação que o torque imprime ao corpo tem o mesmo sentido e a mesma direção que a aceleração angular.
Passo 2
Para encontrarmos o torque resultante, fazemos a soma vetorial dos torques de cada força:
Vamos calcular um por um. Já vamos fazendo a conta e fazendo a regra da mão direita para definirmos o sentido da rotação.
Para , temos que:
Em :
Já para :
No entanto, a linha de ação da força passa pelo eixo de rotação, logo:
Passo 3
Reunindo os resultados:
Agora, precisamos do valor do momento de inércia do cilindro em relação ao centro de massa dele. Este valor é tabelado e vale:
Substituindo os valores de e :
Passo 4
Por último, temos:
E então:
Resposta
a)
b) Visto da face da frente do cilindro, a aceleração angular está no sentido anti-horário.