A figura abaixo mostra as partículas 1 e 2, ambas de massa , presas às extremidades de uma barra rígida de massa desprezível e comprimento , com e . A barra é mantida horizontalmente no fulcro até ser liberada. Qual é o módulo da aceleração inicial (a) da partícula 1 e (b) da partícula 2?
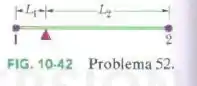
Passo 1
O caminho para a resolução dessa questão será:
- Encontrar o torque total que age no corpo
- Encontrar a aceleração angular da barra (que é a mesma para todos os pontos)
- Encontrar a aceleração linear de cada partícula.
Mãos à obra!
Passo 2
Como a barra não tem peso, as únicas forças que agem nesse sistema são os pesos das partículas 1 e 2, ambos, como sempre, apontando para baixo.
Ficou fácil! Vamos lá:
Se ligou que o peso é perpendicular ao vetor direção? Isso significa que o seno entre os dois vetores é sempre , portanto:
E então usamos a regra da mão direita para saber o sentido do torque. Nunca esquecendo de definir um sentido para ser o positivo. Usaremos aqui o eixo saindo da tela como positivo.
Vamos lá: o torque realizado pelo peso da partícula 1 é, portanto, positivo. Já o da partícula 2 é negativo.
Reunindo os resultados:
Passo 3
Para encontrar a aceleração angular, temos que primeiramente encontrar o momento de inércia do sistema.
Sabendo que a barra tem massa desprezível:
E então:
Usando a relação do torque com a aceleração angular:
E podemos, finalmente, isolar o :
Passo 4
Agora é fácil encontrarmos o que é pedido, só lembrar lá da cinemática:
E então, para cada partícula, temos:
Substituindo os valores no SI:
Resposta
a)
b)