
A lança ilustrada abaixo tem comprimento e massa . Considere a massa uniformemente distribuída. Ela estaria livre para girar, sem atritos, em torno do seu eixo localizado na extremidade inferior (A), contudo, duas forças a mantém em equilíbrio estático fazendo um ângulo com a horizontal. Uma delas tem módulo , está inclinada de em relação à horizontal e atua no centro de massa da lança (B). A outra força tem módulo e atua verticalmente para baixo na extremidade superior da lança (C). Utilize para a aceleração da gravidade.
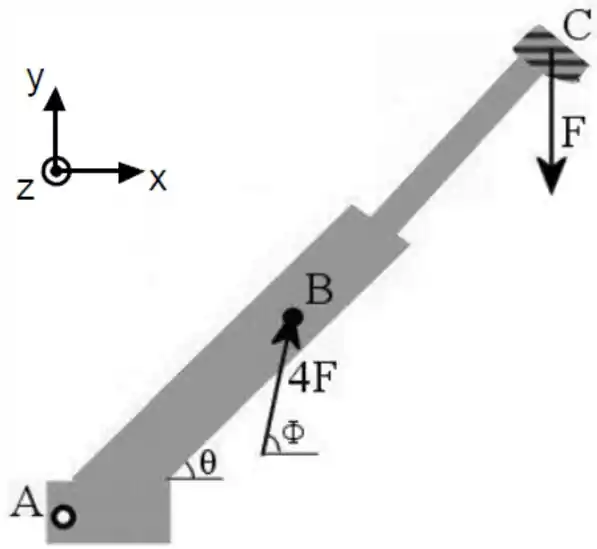
a) Determine os vetores torque em torno de A, produzidos na lança por cada uma das forças e .
b) Suponha agora que as forças e parem de atuar e a lança começa a girar pela ação da força da gravidade. Determine o valor da aceleração angular quando ela passar pela posição horizontal.
c) Continuando seu movimento de rotação, a lança passa pela posição vertical. Determine o valor da velocidade angular nesta posição.
Passo 1
a)
O torque da força em relação ao eixo passando pelo ponto A é:
Então vamos ver na figura qual é o braço da alavanca :
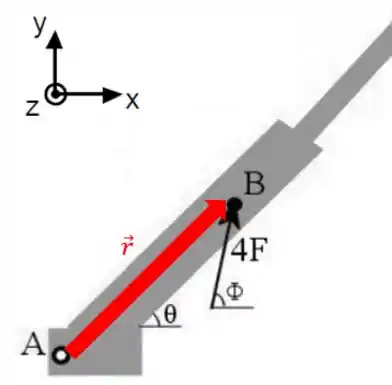
A força está inclinada em relação a , então vamos ter que decompô-la, pra uma das suas componentes fazer um ângulo de com .
Passo 2
Vamos decompor em uma componente , perpendicular a , e , componente paralela a :
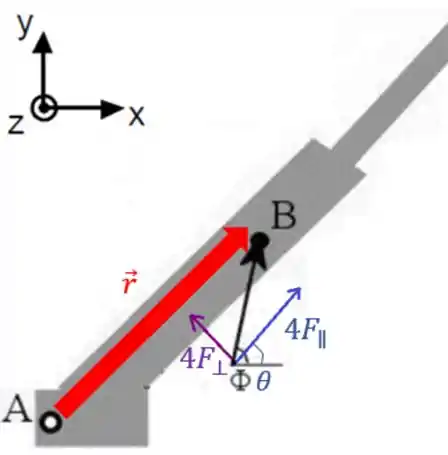
O ângulo entre a horizontal e é , e o ângulo entre e é , então o ângulo entre é .
E é paralela ao vetor , então o ângulo entre e também é !
E é justamente desse ângulo entre o braço da alavanca e a força que a gente precisa calcular o torque. Então o seu módulo é dado por:
Isso se deve ao fato que a componente da força que é paralela ao braço não realiza torque!
Passo 3
A lança tem comprimento e o ponto B está bem na metade dela, então
E pela regra da mão direita, o vetor torque aponta na direção do vetor , logo:
Passo 4
Agora vamos pra força !
O seu torque em relação a A é dado por:
O raciocínio vai ser exatamente o mesmo que pra força : precisamos achar o ângulo entre e , e o torque vai ser:
Porque novamente, só a componente da força que é perpendicular ao braço da alavanca é que produz torque.
Passo 5
O vetor posição (braço) é:
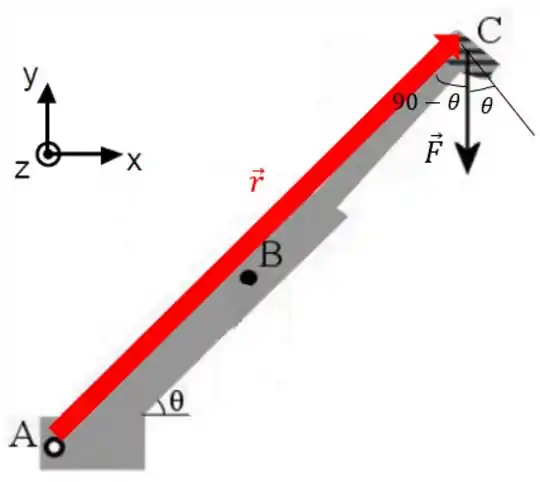
Olhando a figura, podemos ver que o ângulo que a gente tá procurando, entre e , é .
Passo 6
Portanto, o torque é:
Agora o módulo do braço da alavanca é o comprimento todo da lança, :
E o torque é:
A gente até poderia deixar assim, mas esse dá pra simplificar, então é melhor.
Passo 7
Agora tem que estar com a trigonometria em dia! Vamos ver o que vale .
Pra isso uma boa é montar o círculo trigonométrico. Eu sempre faço isso na hora da prova, desenho ele no cantinho da folha.
Vamos ter:
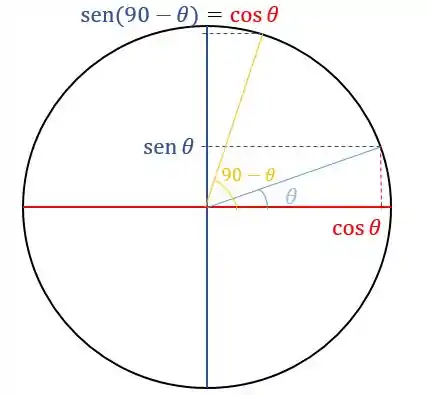
Olhando a figura com carinho, podemos ver, que nem eu botei ali em cima, que
Passo 8
Logo,
Passo 9
b)
Agora as forças e vão parar de atuar e a lança vai cair. Vamos estudar o momento em que ela passa pela posição horizontal. A questão pediu a aceleração angular da lança nesse instante.
Repare que a única força produzindo torque é a força da gravidade (peso), então
Nada mais justo que usar a fórmula:
é o momento de inércia da lança em relação ao eixo que passa por A :)
Passo 10
O torque da força da gravidade em relação ao eixo passando por A é:
A força da gravidade atua no centro de massa da lança, que fica bem no meio dela:
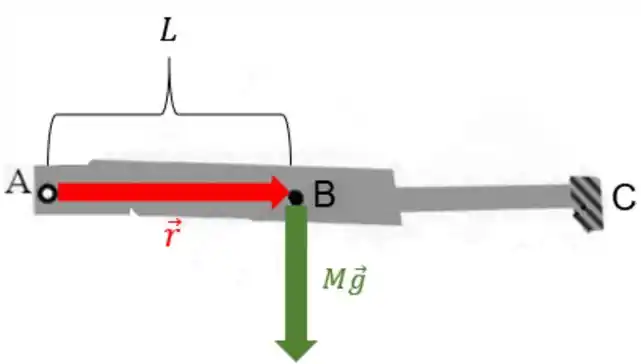
É bom de vez em quando calcular um torque com a força e o sendo perpendiculares né! rs
Enfim, vamos ter
Passo 11
Só falta calcular o momento de inércia da lança em relação ao eixo que passa por A!
O enunciado dá o momento de inércia de uma haste (como nossa lança), em relação ao eixo passando pelo centro de massa:
Mas atenção, isso é pra uma massa e um comprimento genéricos e . No caso do exercício, a massa da lança realmente é mas o comprimento é .
Então
Passo 12
Mas precisamos do momento de inércia em relação ao eixo passando por A. Então vamos aplicar o teorema dos eixos paralelos:
sendo a distância entre os eixos, que é .
Ou seja,
Passo 13
Recapitulando, achamos
Juntando tudo, obtemos:
Passo 14
c)
A aceleração da lança varia com o tempo, então não podemos usar as equações do movimento circular uniformemente variado. Vamos resolver essa questão usando conservação de energia!
Não há atrito ou outra força não-conservativa atuando na lança, então podemos aplicar a conservação da energia mecânica:
Passo 15
A energia mecânica é a soma da energia cinética com a energia potencial . Aqui o movimento é de rotação, então a energia cinética é de rotação (), e a energia potencial é só gravitacional (não tem elástica), então:
Sendo o momento inicial, quando a lança é solta do repouso, e o momento final, quando a lança passa pela posição vertical, isso dá:
Mas a lança parte do repouso! Então
Passo 16
A energia cinética de rotação da lança em torno do eixo que passa por A é:
Sendo a velocidade angular final da lança, que é o que a gente quer achar nessa questão, temos:
Passo 17
Agora vamos dar uma olhada na energia potencial gravitacional.
A primeira coisa que temos que fazer é definir uma altura onde a vale zero. E a altura mais evidente é a do ponto A, que é a do eixo de rotação. Então vamos fixar , show?
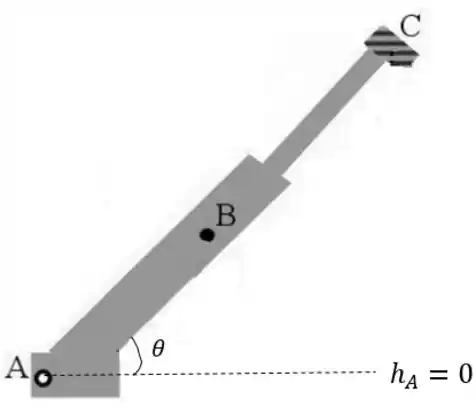
Passo 18
A altura que a gente tem que considerar pra medir a energia potencial gravitacional da lança é a do centro de massa dela, o ponto B.
Vamos começar achando a altura inicial do ponto B, quando ela está inclinada.
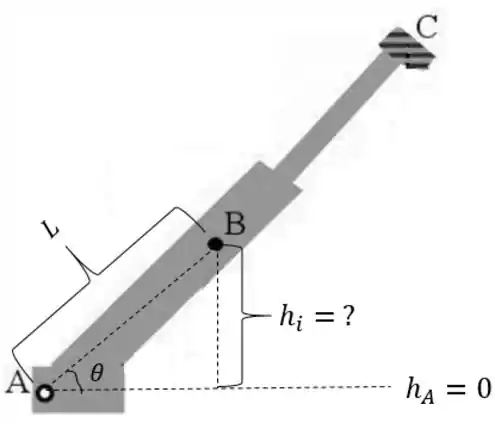
Olhando a figura com a carinho, e aplicando uma trigonometria básica, obtemos:
Então a energia potencial gravitacional inicial é:
Passo 19
Agora vamos ver qual é a altura final do centro de massa da lança, quando ela está na vertical.
Na verdade, justamente por estar na vertical, e apontando pra baixo, essa altura simplesmente é :
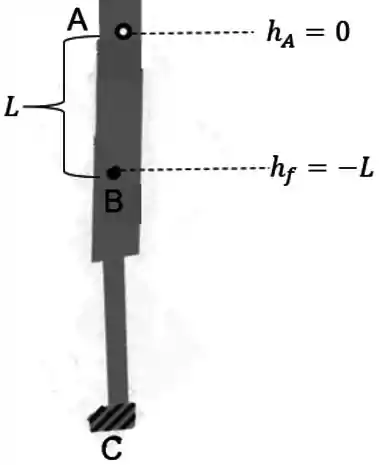
Então a energia potencial gravitacional final é:
Passo 20
Show! Vamos voltar à equação de conservação de energia mecânica:
Resposta
a)
b)
c)