Questão discursiva.
A figura abaixo mostra duas partículas de massa e presas às extremidades de uma barra rígida de massa desprezível e comprimento , com e .
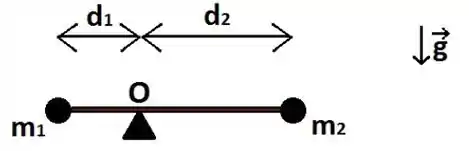
A barra é mantida fixa horizontalmente sobre o ponto , até ser liberada. A partir de então, a barra pode girar em torno de um eixo que passa pelo ponto , perpendicular ao plano da página.
Use .
- Calcule o momento de inérica do sistema em relação ao referido eixo.
- Calcule o módulo do torque resultante em relação ao ponto .
- Determine o módulo da aceleração tangencial de cada partícula assim que a barra é liberada.
Passo 1
Letra a)
Como a barra tem massa desprezível, ela não contribui para o cálculo do momento de inércia. Ficamos apenas com duas partículas.
Onde é a distância da partícula até o eixo de rotação.
Passo 2
Letra b)
O torque resultante vai ser a soma dos torques de cada partícula.
A contribuição de cada partícula se deve à sua força gravitacional, e assim:
Nas equações, não aparece o seno do ângulo, pois o ângulo é e . O vetor unitário é do eixo que passa por , tendo seu sentido saindo da tela e indo em direção à você, leitor. Por isso o sinal de menos da segunda equação, indicando que a barra giraria no sentido horário.
Assim, em módulo:
O sinal apenas indica que a rotação seria no sentido horário.
Passo 3
Letra c)
A versão “dinâmica de rotação” da segunda lei de Newton é:
Onde é a aceleração angular, que pode ser relacionada com a aceleração tangencial de cada partícula. Em módulo, temos:
Para passar para a aceleração tangencial das partículas, multiplicamos pelas suas distâncias do eixo.
Resposta
Letra a)
Letra b)
Letra c)