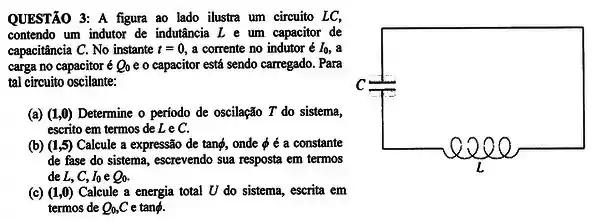
Passo 1
Letra (a). O período de oscilação de um circuito na ressonância é encontrado quando igualamos as reatâncias capacitivas e indutivas:
Passo 2
Letra (b). A ideia é entender que tanto a corrente quanto a carga podem ser expressas em termos de uma função senoidal, oscilatória:
Então:
Dessa forma:
Passo 3
Letra (c). A soma da energia do capacitor com o indutor em qualquer instante fornece a energia total. Essa energia se distribui de maneira cíclica entre esses dois elementos.
Agora é fazer algumas substituições malandras para expressarmos as coisas em função das variáveis que o problema pediu:
Logo:
Somando isso com a energia do indutor:
No instante :
Mas, lembrando:
Substituindo :
Resposta
Letra (a)
Letra (b)
Letra (c)
Exercícios de Livros Relacionados
Um indutor é ligado a um capacitor cuja capacitância pode ser ajustada através de um botão. Queremos que a frequência deste circuito LC varie linearmente com o ângulo de rotação do botão, de 2 × 10 5
Se a tensão rms em um circuito ac é duplicada, a tensão de pico é a duplicada. b reduzida a metade. c aumentada por um fator 2 . d permanece inalterada.
Considere que você aumenta a taxa de rotação da bobina no gerador mostrado no circuito simples na figura 29 - 29 . Então, a corrente rms a aumenta b não varia c pode aumentar ou diminuir dependendo da
35- ( a ) Aplicando as equações ( 30.21 ) e ( 30.23 ) para um circuito L - C , escreva expressões para a energia armazenada em um capacitor em função do tempo e para a energia armazenada em um indutor
37- Mostre que sqrt(L C) possui unidades de tempo.