No circuito abaixo, o capacitor tem uma capacitância e foi inicialmente carregado a uma diferença de potencial com a polaridade indicada na figura. Ele forma uma espira retangular, de lados e ao ser ligado em série a um resistor de resistência e a uma chave . A espira menor tem dimensões e , está afastada da espira maior por uma distância , possui voltas e é composta de um fio cuja resistência por unidade de comprimento vale . A figura não está desenhada em escala e é assumido que somente o fio da espira grande, mais próximo da espira pequena, produz campo magnético apreciável sobre esta (, e , portanto pode ser considerado um fio muito longo). Para todas as perguntas abaixo, desconsidere o fluxo criado pela bobina menor na bobina maior, bem como o fluxo criado pela bobina maior nela mesma. Nestas condições, encontre
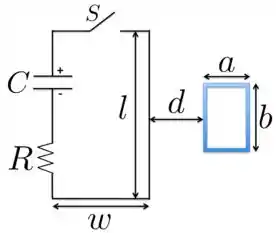
- A corrente na espira maior em função do tempo depois que a chave é fechada;
- O sentido da corrente induzida na espira menor (indique na figura e justifique);
- A corrente induzida na espira menor em função do tempo depois que a chave foi fechada.
Passo 1
a) Vamos aplicar a lei das malhas a malha do circuito. Fazendo isso, teremos
em que usamos . Resolvendo a integral acima, teremos que
Quando a chave S é ligada, em , o capacitor tinha uma carga total de . Substituindo isso na expressão acima
Derivando com relação ao tempo, temos
que mostra que a corrente no circuito decresce exponencialmente com o tempo.
Passo 2
b) O campo magnético gerado pela corrente na espira menor que encontramos está saindo do plano da página e é perpendicular a ela. No entanto, essa corrente está diminuindo com tempo, o que significa que fluxo magnético correspondente através da espira menor também está diminuindo com o tempo.
Como esse fluxo devido ao campo produzido por diminui com o tempo, vai aparecer uma corrente induzida no sentido anti-horário, o que produzirá um campo induzido cujo fluxo magnético se opõe à diminuição do fluxo devido a .
Passo 3
c) Para resolvermos este item, vamos olhar para a figura abaixo, em que apenas consideramos o fio “infinito” de comprimento () e a espira menor que possui voltas.
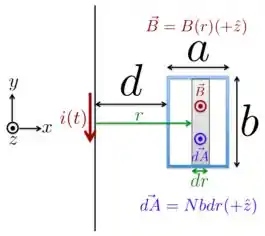
O campo magnético produzido pela corrente da espira maior à uma distância do fio tem módulo dado por
Portanto, se o vetor área da espira menor é paralelo ao campo, então o fluxo magnético total através da espira menor (que tem espiras!) será:
que dá como resultado um fluxo igual a
Passo 4
c) Continuação…
A fem induzida será
Derivando a corrente que encontramos no Passo 1,
Substituindo em , temos
Como , isso significa que a corrente está no sentido anti-horário, já que, por causa da nossa escolha de saindo do plano da página o sentido positivo o anti-horário, como já tínhamos concluído no item b.
Passo 5
c) Continuação…
Agora que já encontramos a fem induzida, podemos achar também a corrente induzida . Para isso, temos que nos lembrar que
em que é a resistência total da espira menor.
Como o problema diz que a resistência por unidade de comprimento da espira menor é e ela tem voltas, então, o seu comprimento total é e a sua resistência vale
Fechando, a corrente induzida é, finalmente,
Resposta
- A corrente induzida na espira menor tem sentido anti-horário;