Considere o circuito da figura 1 onde , , , , e ocorrem as seguintes fases sucessivas:
Fase1: chave fechada e aberta durante longo tempo
Fase 2: chave aberta e fechada durante longo tempo
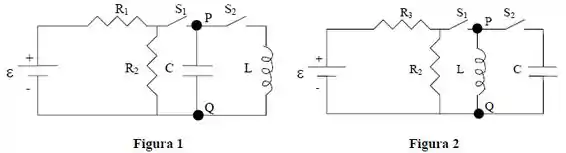
Determine, justificando todas as respostas:
A ddp em função do tempo durante a fase 2.
A corrente no indutor em função do tempo durante a fase 2.
A carga do capacitor em função do tempo durante a fase 2.
A energia do circuito durante a fase 2.
Considere agora que as posições do indutor e do capacitor são trocadas e a resistência é substituída por outra , conforme a Figura 2. Nestas novas condições, determine:
O valor da resistência tal que a energia do circuito seja igual ao da Figura 1.
Se o indutor no circuito da Figura 1 tem uma resistência interna , após quanto tempo a energia inicial do circuito decai de , sendo “ a base dos logaritmos naturais.
Passo 1
A ddp em função do tempo durante a fase 2.
Determinar a ddp é determinar a ddp do capacitor durante a fase 2.
Durante a fase 2, ao circuito é formado apenas pelo capacitor e pelo indutor. Em um circuito , a carga no capacitor é dada por:
Logo, a ddp no capacitor será:
A ddp máxima no capacitor ocorre quando ele está totalmente carregado. Na fase 1, quando o capacitor está totalmente carregado:
Logo:
Passo 2
Substituindo os valores, teremos:
A frequência de oscilação, para um circuito , corresponde à frequência de ressonância, dada por:
Substituindo os valores, teremos:
Finalmente:
Passo 3
A corrente no indutor em função do tempo durante a fase 2.
Como falamos no passo anterior, a ddp no capacitor é dada por:
Onde , logo:
Por definição, a corrente no indutor será dada por:
Finalmente:
Passo 4
A carga do capacitor em função do tempo durante a fase 2.
Acabamos resolvendo esse cara no passo anterior:
Onde , logo:
Passo 5
A energia do circuito durante a fase 2.
A energia do circuito será dada por:
Onde e , logo:
Passo 6
O valor da resistência tal que a energia do circuito seja igual ao da Figura 1.
Em um circuito , quando , , logo a corrente passa somente pelo indutor, e não mais pelo resistor .
A energia máxima no indutor é dada por:
Assim, o valor de é dado por:
Passo 7
Se o indutor no circuito da Figura 1 tem uma resistência interna , após quanto tempo a energia inicial do circuito decai de , sendo “ a base dos logaritmos naturais.
Em um circuito , a carga no capacito varia de acordo com a equação:
Onde , lembrando que .
A energia no circuito é proporcional ao quadrado da carga no capacitor
E a carga no capacitor é proporcional à seguinte exponencial
Logo:
Para que a energia decaia de , é necessário que:
Logo>
Substituindo os valores de e , teremos:
Resposta