Considere o circuito formado por uma bateria com fem , um resistor com resistência , um capacitor com capacitância , um indutor com indutância e uma chave comutadora com duas posições: e .

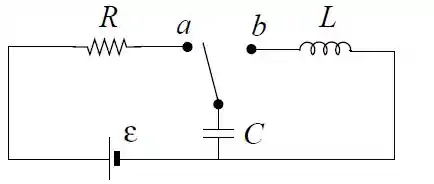
A chave permanece na posição por um tempo muito longo. Nesta situação, em um instante definido como , a chave passa para a posição b.

Qual é a carga na placa superior do capacitor em .

Deduza a equação diferencial para a carga na placa superior do capacitor com a chave na posição . Sabendo que a solução geral da equação diferencial tem a forma , determine . Usando as condições iniciais para o problema determine e .

Determine a energia no capacitor e a energia no indutor como função do tempo. A soma das energias no capacitor e no indutor depende do tempo?

Deduza a equação diferencial para a carga na placa superior do capacitor com a chave na posição . Sabendo que a solução geral da equação diferencial tem a forma , determine . Usando as condições iniciais para o problema determine e .

Quando a chave passa para a posição , o circuito passará a ser formado somente pelo capacitor e pelo indutor. Portanto, de acordo com a Lei das Malhas:

Por definição, , portanto, a equação diferencial será:

Sabendo que a solução da equação diferencial é , vamos aplicar isso à equação diferencial para determinar .

Substituindo isso na equação diferencial

Teremos:

Agora é só organizar esse cara:

Finalmente:

As condições iniciais do circuito são:

Onde:

Então vamos utilizar isso para determinar e , beleza?

Então, daqui podemos tirar que:

Então temos duas possibilidades:

Ou:

Determine a energia no capacitor e a energia no indutor como função do tempo. A soma das energias no capacitor e no indutor depende do tempo?

As energias no capacitor e no indutor são dadas por:

Onde:

Portanto:

Lembrando que , logo:

Substituindo isso na expressão de , teremos:

Somando as energias, teremos:

Logo, a somas das energias no capacitor e no indutor independe do tempo.