Considere o circuito da figura , onde , , , o capacitor e o indutor estão inicialmente sem energia. O circuito é operado nas seguintes fases sucessivas:
Fase : chave fechada e aberta durante longo tempo.
Fase : chave aberta e fechada durante longo tempo.
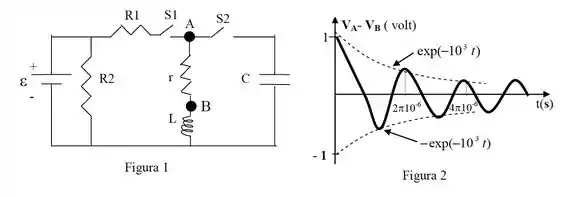
Durante a fase , a d.d.p. em função do tempo corresponde ao gráfico da figura , na qual a escala de tempo no eixo horizontal está expressa em segundos. Supondo que a frequência angular da oscilação amortecida possa ser aproximada pela da oscilação livre sem amortecimento , determine:
O valor da resistência .
O valor da corrente no indutor no final da fase .
O valor da capacitância e da indutância .
A energia dissipada na resistência na fase .
Passo 1
Para determinar a resistência , devemos pensar no fim da fase , pois nesse momento, o indutor se comporta como um fio qualquer e a corrente no resistor é máxima, ou seja, temos:
Já no início da fase , também temos a mesma corrente máxima, só que agora, nos foi fornecida a diferença de potencial nos terminais do resistor para esse instante, , temos então:
Substituindo o valor de , temos:
Substituindo os valores conhecidos:
Passo 2
No fim da fase , o indutor se comporta como um fio qualquer, e nós já sabemos que a corrente nesse instante é máxima, portanto:
Passo 3
Para determinar o valor da capacitância e da indutância, devemos analisar como varia a corrente em função do tempo para um circuito RLC, temos que a corrente varia da seguinte forma:
Pelo gráfico dado, vemos que o expoente da função exponencial é:
Isolando o valor da indutância, temos:
Substituindo o valor da resistência, temos:
Para determinar o valor da capacitância, vamos usar o fato de que a oscilação amortecida pode ser aproximada para uma oscilação livre, onde . Pelo gráfico, vemos que o período de oscilação é:
Ou seja:
Substituindo para achar a capacitância:
Passo 4
Para determinar a energia dissipada na resistência durante a fase dois, devemos calcular a energia armazenada no indutor durante a fase . Como o capacitor está inicialmente descarregado, somente a energia armazenada no indutor será dissipada no resistor, vamos calcular isso:
Resposta
;