No circuito da figura, tem-se , , , e . Inicialmente o capacitor está descarregado e o indutor está sem energia. No circuito, ocorrem as seguintes fases sucessivas:
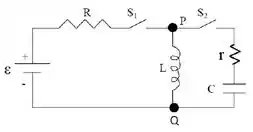
Fase 1: chave fechada e aberta durante longo tempo.
Fase 2: chave aberta e fechada durante longo tempo.
- Encontre a expressão para a corrente no indutor em função do tempo durante a Fase 1.
- Determine o valor do coeficiente de amortecimento , da frequência angular e da fase .
- Escreva a expressão geral para a corrente em função do tempo durante a Fase 2, usando os valores obtidos no item a), assim como os valores para a corrente inicial e para .
- Desenhe o circuito sem a fonte, indicando o sentido da corrente inicial e as polaridades das tensões em todos os seus elementos. Em seguida, determine expressões para as tensões no resistor e no capacitor em função do tempo durante a Fase 2.
Sabe-se que a carga no capacitor durante a Fase 2 tem a seguinte expressão geral (aqui o tempo é medido a partir do fechamento da chave ):
Passo 1
a) Na Fase 1, como a chave está aberta, então temos apenas um circuito . Para esse caso, temos que a corrente varia com o tempo da seguinte maneira:
sendo que é uma constante de tempo indutiva característica do sistema e é o maior valor que corrente pode alcançar no circuito.
Jogando os valores que o problema fornece, teremos
Nessa expressão é a unidade Ampère para a corrente.
Passo 2
b) Nesse caso, é importante nos lembrarmos de como são escritas as quantidades que entram na expressão para a carga . A primeira delas é a constante de amortecimento :
em que já substituímos os valores do problema.
A outra quantidade é a frequência angular :
Agora, para finalizar, precisamos encontrar a fase . Precisamos ver como é carga no instante inicial. Mas o problema disse que, inicialmente, a carga inicial do capacitor é zero. Por isso, logo que fechamos a chave , a carga inicial do capacitor é igual a zero:
Com essa fase, podemos reescrever a carga do capacitor como
Passo 3
c) Agora basta derivarmos a carga com relação ao tempo para encontrarmos a corrente:
A corrente em da Fase 2 será igual ao valor da corrente máxima do final da Fase 1. Portanto,
Podemos encontrar também como fica a carga
Substituindo na expressão , teremos
Simplificando um pouco mais essa expressão, teremos
Agora, como o segundo termo do lado direito da igualdade é um termo pequeno, em comparação com o primeiro, então podemos reescrever a expressão da corrente como
Passo 4
d) Na Fase 2, como temos a chave aberta, sobra apenas o circuito da malha à direita, mas com a chave fechada. Para essa situação, temos que a corrente está no sentido anti-horário e as polaridades são as que estão mostradas na figura abaixo.
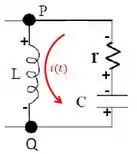
Vamos para as voltagens através dos elementos do circuito.
A voltagem entre os terminais do capacitor é
Através do resistor, teremos que