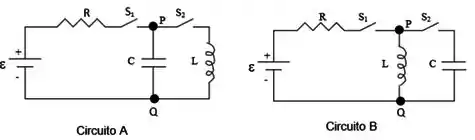
Nos circuitos e das figuras tem-se , , e , sendo que o capacitor e o indutor estão inicialmente sem energia. Nestes circuitos também ocorrem as seguintes fases sucessivas:
Fase : chave fechada e aberta durante longo tempo.
Fase : chave aberta e fechada durante longo tempo.
Com os dados a sua disposição:
Escreva a expressão da d.d.p () em função do tempo no circuito durante a Fase . Esboce também o seu gráfico nas fases e , indicando o valor no início da Fase e no início da Fase .
Escreva a expressão da d.d.p () em função do tempo no circuito durante a Fase . Esboce também o seu gráfico nas fases e , indicando o valor no início da Fase e no início da Fase .
Imagine agora que o indutor no circuito seja substituído por outro com o mesmo valor de mas cujo fio das espiras tem uma resistência total de . Escreva neste caso a expressão da d.d.p () em função do tempo durante a Fase . Faça um esboço de seu gráfico na Fase .
Passo 1
Para o circuito , temos que a fase corresponde a um circuito RC, onde o capacitor está sendo carregado, e a fase corresponde a um circuito LC, onde a corrente oscila por conta da presença do indutor.
Na Fase , temos que a d.d.p nos terminais do capacitor varia de até o valor máximo .
Agora vamos ao que interessa, a fase . Durante essa fase, temos um circuito LC, nele, a carga do capacitor varia da seguinte maneira:
Onde é a carga inicial, ou seja, a carga do capacitor ao final da fase , esse valor é dado por:
Tendo em vista que , temos que a d.d.p nos terminais do capacitor varia da seguinte maneira:
Onde e . Substituindo os valores conhecidos:
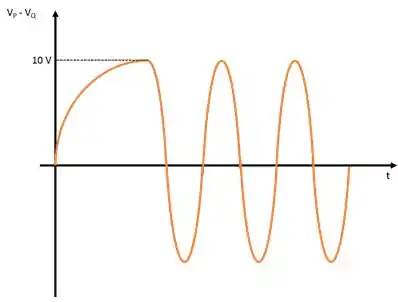
Portanto, a d.d.p no início da fase é e a partir desse momento a d.d.p varia periodicamente, como indicado no gráfico abaixo:
Passo 2
Durante a fase , temos um circuito RL, nesse circuito, temos que a corrente varia da seguinte maneira:
Para , temos que a corrente é nula, ou seja, temos que a d.d.p nos terminais do indutor será , pois o resistor não contribuirá (. E depois de um longo tempo, temos que o indutor se comporta como um fio comum, ou seja, a d.d.p em seus terminais será nula.
Agora vamos para a fase . Nessa fase temos um circuito LC, nele, temos que a corrente varia da seguinte forma:
Onde é a corrente final da fase , ou seja, e como a corrente inicial na fase vale , temos que
Além disso, . A d.d.p nos terminais de um indutor é dada por:
Derivando a equação da corrente:
Substituindo os valores, temos:
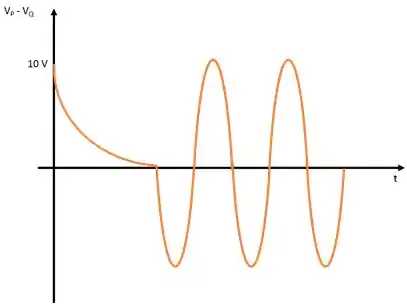
Portanto, temos que a d.d.p inicial na fase é nula e a partir desse momento, ela irá oscilar periodicamente, como apresentado no gráfico abaixo.
Passo 3
Agora, iremos voltar à situação do circuito , no entanto temos agora que o fio do indutor apresenta uma resistência total de . Na fase , não temos nenhuma alteração. Na fase , passamos a ter um circuito RLC, ou seja, um circuito com oscilação amortecida, para esse circuito, temos que a carga no capacitor varia da seguinte maneira:
Onde , substituindo os valores, temos:
Repare que o segundo termo dentro da raiz pode ser desprezado por ser muito pequeno em relação ao primeiro termo. Além disso, temos que , pois a carga inicial no capacitor é . Temos então que na fase a d.d.p inicial é e ela irá variar periodicamente com oscilação amortecida conforme o gráfico abaixo.
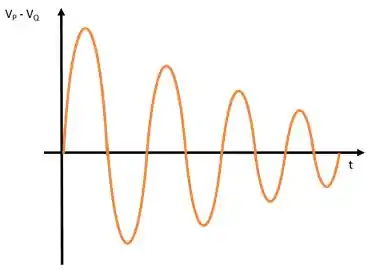
Resposta