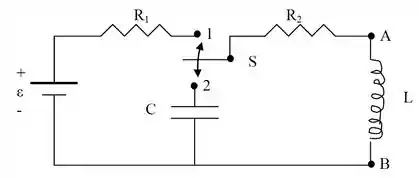
Considere o circuito da figura onde , , , e . Neste circuito ocorrem as seguintes fases sucessivas:
Fase : chave na posição durante longo tempo.
Fase : chave comutada instantanemanere da posição para a posição , permanecendo nesta posição durante longo tempo.
A intensidade e o sentido da corrente no indutor em função do tempo durante a Fase .
A d.d.p em função do tempo durante a Fase .
A energia armazenada no indutor no final da Fase .
A corrente no indutor em função do tempo na Fase , indicando o sentido no início desta fase ( imediatamente após a comutação da chave da posição para a posição ).
As d.d.p. , e no início da Fase .
Quais seriam os efeitos na corrente do indutor durante a Fase se os valores de e forem trocados para e , respectivamente?
Passo 1
Durante a fase , temos um circuito RL. Para esse tipo de circuito, temos que a corrente varia da seguinte maneira:
No caso acima, temos que a resistência equivalente é a soma das resistências, tendo em vista que os resistores estão em série. Logo, a corrente em função do tempo será:
A corrente flui do polo positivo para o negativo, ou seja, sentido horário.
Passo 2
A d.d.p nos terminais de um indutor é dada pela seguinte relação:
Logo:
Passo 3
A energia armazenada em um indutor é dada pela seguinte relação:
Substituindo, temos:
Passo 4
Em circuito , temos que a corrente, irá fluir no sentido anti-horário, pois a energia está armazenada no indutor. A corrente para esse circuito é dada pela seguinte relação:
Onde
Substituindo os valores, temos:
Passo 5
Como o capacitor está inicialmente descarregado, a d.d.p entre seus terminais será nula, logo:
Logo a d.d.p nos terminais do indutor e nos terminais do resistor será igual em módulo, para o resistor, como a corrente inicial vale :
E no indutor, a d.d.p será:
O valor é negativo por conta da Lei das malhas(a soma deve dar zero)!
Passo 6
Ao trocar o valor das resistências, temos que o se torna um número imaginário, pois:
Portanto, se trata de uma oscilação superamortecida.
Resposta
Oscilação superamortecido.