Considere o circuito da figura, onde os valores dos componentes são conhecidos: , , , e .
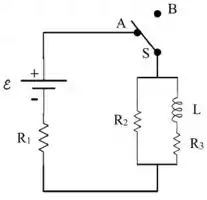
Fase 1: chave na posição A
Fase 2: chave na posição B
- Encontre as intensidades e os sentidos (para cima ou para baixo) das correntes em , e imediatamente depois de fechar a chave S na posição A (início da fase 1).
- Encontre as intensidades e os sentidos (para cima ou para baixo) das correntes em , e no final da fase 1.
- Encontre as intensidades e os sentidos (para cima ou para baixo) das correntes que passam em , e imediatamente depois de fechar a chave S na posição B (início da fase 2).
- Encontre as intensidades e os sentidos (para cima ou para baixo) das correntes que passam em , e no final da fase 2.
- Encontre a energia dissipada em cada um dos resistores , e a partir do momento que a chave S é fechada na posição B e permanece nesta posição por um tempo muito longo. (Nota: pode deixar seu resultado em termos de frações numéricas, sem necessidade de calculá-las).
Após um tempo muito longo, a chave S é colocada na posição B (fase 2).
Passo 1
a) No instante logo após a chave ser colocada na posição A, não passa corrente no indutor e, consequentemente, não passa corrente também no resistor que está em série com ele. Por isso
Por isso, a corrente que passa no circuito sai da bateria no sentido do polo negativo para o positivo e passa de baixo para cima no resistor e no sentido de cima para baixo no que está em série com em .
O valor dessa corrente é:
Passo 2
b) Quando passa um tempo muito grande, ou seja, , então a corrente que passa pelo indutor chega ao seu valor máximo . Portanto, a ddp no indutor é zero, já que
ou seja, a corrente não varia mais com o tempo. Como não há queda de potencial através do indutor, a ddp nesse trecho é somente aquela devida a ddp no resistor quando ele é percorrido por uma corrente . Queremos encontrar esta corrente e também aquele que passa pelo resistor .
Como esses dois resistores estão ligado em paralelo, eles estão à mesma ddp, ou seja,
Como estão em paralelo, podemos “substitui-los” por uma resistência equivalente de . Como está em série com o , a corrente que passa no circuito em é
Essa corrente é igual a soma das correntes e que passam, respectivamente, nos resistors e . Portanto, como , temos
Logo, também teremos que
Nesse caso, a corrente passará de baixo para cima em e de cima para baixo em ambos e .
Todos os valores que encontramos para as correntes acima são para um tempo muito grande, ou seja, para quando a chave está na posição A do circuito.
Passo 3
c) No instante da chave na posição B, não tem mais corrente em , ou seja,
Como a corrente no indutor é máxima e igual a , a corrente em é também .
Como o valor da corrente que passa pelo resistor é zero, então a corrente que passa nos resistores e são iguais. Por isso, o que temos, nesse instante em que a chave é ligada na posição B, é
que tem sentido de cima para baixo em e de baixo para cima em . Note que, nesse caso, a corrente vai ficar circulando apenas na malha que contém os resistores e .
Passo 4
d) Para um tempo muito grande após a chave ser colocada na posição B, as correntes vão se anular, por isso temos que
No caso da chave ligada na posição B, não há mais corrente que passa pelo resistor em nenhum momento. Por isso, para todo instante de tempo
e a corrente passa apenas no circuito reduzido que tem o indutor e os dois resistores e em série. Portanto, no tempo logo após a chave estar na posição B, teremos que
Para um tempo intermediário depois da chave na posição B, corrente que passa nos resistores será
em que a constante indutiva é dada por
o que nos dá
Passo 5
e) A energia total dissipada em será
que dá como resultado final
Para , a energia total dissipada será
e teremos
Apenas para completar, a energia que o indutor tinha em logo após a chave ser mudada para B era de
que é igual a
ou seja, toda a energia que havia no campo magnético do indutor foi dissipada através dos resistores e .
Resposta
- Corrente de baixo para cima em e de cima para baixo em ; em ambos, a corrente é
- correntes no mesmo sentido do item a) ;