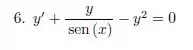
Passo 1
A primeira coisa é identificar se nossa equação é linear de primeira ordem. Os pré-requisitos para isso são:
Para ser de primeira ordem a derivada de maior ordem deve ter ordem 1.
Bom, de primeira ordem ela é. Mas para ser linear:
- Tanto as derivadas de quanto o próprio não podem estar elevados ao quadrado, cubo ou qualquer outro expoente diferente de 1.
- Os coeficientes que aparecem multiplicando as derivadas de e o próprio dependem apenas de .
No nosso caso temos um ali, então essa equação não é linear.
Resposta
Exercícios de Livros Relacionados
Resolva a equação diferencial.y^' = (e^y)/(x y)
Resolva a equação diferencial:y^' = x e^(x - y) c o s s e c y
Resolva o problema de valor inicial.t (d u)/(d t) = t^2 + 3 u , t0 , u (2) = 4
Determine se a equação diferencial é linear.x y + sqrt(x) = e^x y '
Determine se a equação diferencial é linear.x y^' + ln x - x^2 y = 0