![]()
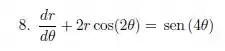
Passo 1
A primeira coisa é identificar se nossa equação é linear de primeira ordem. Os pré-requisitos para isso são:
Para ser de primeira ordem a derivada de maior ordem deve ter ordem 1.
Ok, de primeira ordem ela é. Mas para ser linear:
- Tanto as derivadas de quanto o próprio não podem estar elevados ao quadrado, cubo ou qualquer outro expoente diferente de 1.
- Os coeficientes que aparecem multiplicando as derivadas de e o próprio dependem apenas de .
Está tudo de acordo, temos uma equação linear de primeira ordem.
Passo 2
Agora vamos resolvê-la. Essa não é uma EDO separável. E agora?
Perceba que ela tem esse formato:
Vamos identificar e
Passo 3
Identificamos qual tipo de equação temos e já achamos quem são e . O próximo passo é calcular a integral
Vamos utilizar a substituição
Então ficamos com
Passo 4
A próxima coisa é calcular o fator integrante
No nosso caso
Passo 5
Agora precisamos calcular a integral
Podemos primeiro substituir
E para resolver, vamos utilizar a substituição
Concentra aqui e olha como vai ficar
Isso aqui em baixo não é uma notação formal ok? É só para conseguirmos entender todos os passos.
Vamos fazer uma última substituição pra ter a integral toda escrita em termos de . Partindo de:
Se aplicarmos o dos dois lados, temos:
Então a integral fica:
Para resolver essa integral, podemos usar integração por partes. Vamos usar a notação e .
Usando a formulinha da integração por partes
Desfazendo a substituição lá de cima
Então
Passo 6
Finalmente chegamos no fim, agora só falta colocar tudo na solução
Prontinho!
Resposta
![]()