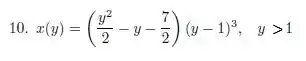Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de EDO Linear de 1ª Ordem

Ver Teoria
Exercício 891234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878890919293949596979899100

Enunciado

Passo 1

A primeira cosia que precisamos é determinar que tipo de EDO é essa.

y - 1 x ' - 3 x = y - 1 5

Se dividirmos a equação inteira por ( y - 1 ) , ficamos com

x ' - 3 x y - 1 = y - 1 4

Perceba que essa equação está no formato

y ' x + A x y x = B ( x )

Então agora já sabemos o mecanismo para resolver.

Passo 2

Primeiro precisamos identificar A y e B ( y )

A y = - 3 ( y - 1 )

B y = y - 1 4

Passo 3

O próximo passo é calcular a integral

∫ A y d y = ∫ - 3 ( y - 1 )   d y

= - 3 ∫ 1 ( y - 1 ) d y

Vamos utilizar a substituição

u = ( y - 1 )

d u = d y

Então ficamos com

- 3 ∫ d u u = - 3 ln ⁡ u

= ln ⁡ u - 3

= ln ⁡ y - 1 - 3

∫ A y d y = ln ⁡ y - 1 - 3

Repara que y - 1 tá dentro do logaritmo! Precisamos ter:

y - 1 > 0

y > 1

Passo 4

A próxima coisa é calcular o fator integrante

I y = e ∫ A y d y

No nosso caso

I y = e ln ⁡ y - 1 - 3

Ou seja

I y = y - 1 - 3

Passo 5

Agora precisamos calcular a integral

∫ I y B ( y ) d y = ∫ y - 1 - 3 y - 1 4 d y

= ∫ ( y - 1 ) d y

Podemos separar em duas integrais

∫ ( y - 1 ) d y = ∫ y   d y - ∫ d y

Integrando ficamos com

∫ I y B ( y ) d y = y 2 2 - y

Passo 6

E só falta colocar tudo na solução

x y = 1 y - 1 - 3 y 2 2 - y + C

x y = y - 1 3 y 2 2 - y + C

Maaas, temos um caso de Problema de valor inicial.

x - 1 = 16

Aplicando na nossa solução

x - 1 = - 1 - 1 3 ( - 1 ) 2 2 - ( - 1 ) + C

Resolvendo, encontramos que

C = - 7 2

Então nossa solução final é

x y = y - 1 3 y 2 2 - y - 7 2

Resposta

Exercícios de Livros Relacionados

Resolva a equação diferencial.y^' = (e^y)/(x y)
Resolva a equação diferencial:y^' = x e^(x - y) c o s s e c y
Resolva o problema de valor inicial.t (d u)/(d t) = t^2 + 3 u , t0 , u (2) = 4
Determine se a equação diferencial é linear.x y + sqrt(x) = e^x y '
Determine se a equação diferencial é linear.x y^' + ln x - x^2 y = 0