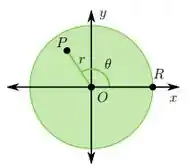
01) A temperatura de equilíbrio em um ponto de uma chapa circular feita com um material uniforme pode ser escrita em função das coordenadas polares , de , onde é a distância entre o ponto e a origem e é o ângulo formado entre o eixo e o segmento . Temos que varia em e que varia em , onde é o raio da chapa. Note que o conjunto dos pontos tais que é constante formam uma circunferência.

Escrevendo a temperatura em como produto de duas funções , é possível mostrar que as funções e satisfazem as seguintes equações diferenciais:

Onde é uma constante positiva. O objetivo dessa questão é resolver essas duas equações diferenciais e estudar suas soluções.

a) Mostre que satisfaz a equação . Determine os valores de tais que e são soluções fundamentais dessa equação.

b) Use o fato de que e representam o mesmo ponto na chapa, para concluir que . Use esse fato para concluir que , para algum inteiro .

c) Mostre que satisfaz a equação , , conhecida como equação de Euler. Determine os valores de tais que é solução da equação de Euler.

d) Use o item anterior para obter a solução geral da equação de Euler. Verifique que qualquer solução que não é proporcional à solução possui assíntota vertical em .

b) Basicamente, nesse item precisamos demonstrar duas coisas:

para algum inteiro .

Para nos ajudar, a questão fala que e representam o mesmo ponto na chapa .

Beleza, mas como podemos usar essa informação?

O negócio é pensar que, como representam o mesmo ponto, a temperatura é a mesma. Sabemos que a temperatura no ponto P é dada por

Assim, teremos:

Como vale para todo , tem que ser válido:

Top! Conseguimos mostrar a primeira parte.

Lembra agora que no item a encontramos duas soluções ditas soluções fundamentais? Isso significa que podemos escrever uma solução geral como sendo:

Daí, temos:

Como isso tem que ser válido para qualquer solução, ou seja, para qualquer e , podemos escolher os mais convenientes. Assim, tomando e , vem:

Logo, deve ser um múltiplo inteiro de . O que nos permite escrever:

Onde .

Por fim, chegamos que:

Que é exatamente o que queríamos mostrar 😊

c) Então galera, nesse item precisamos fazer duas coisas também:

1. Mostrar que satisfaz a equação
2. Determinar para que seja solução de da EDO acima.

Bom, vamos começar pela primeira parte. Por causa do enunciado, nós sabemos que:

Lembrando que no item anterior, mostramos que . Daí, substituindo, temos:

Perfeito! Já mostramos a primeira parte.

Agora, para determinar os valores de que fazem solução da EDO, o que podemos fazer?

Então, a ideia quando queremos determinar soluções pelo “chute” é substituirmos na EDO e ver o que acontece. Bora lá!

Não faz sentido termos , então devemos ter:

Com isso, temos duas soluções possíveis:

Prontinho 😊

Calma galerinha, já estamos no último item uhuuul!

d)

Precisamos primeiramente determinar a solução geral da EDO em , chamada equação de Euler. Bora começar verificando se as soluções e são fundamentais. Como vimos no item b, basta verificar se . Assim:

Portanto, essas soluções são fundamentais. Assim, podemos escrever a solução geral de como sendo uma combinação linear delas. Logo:

Excelente! A primeira parte já foi.

Agora pra encerrar de vez essa questão, devemos mostrar que qualquer solução que não é proporcional a possui assíntota vertical em .

Beleza, pensa comigo, nós acabamos de encontrar que:

Daí, se a solução não é proporcional a , devemos ter . Logo, quando tende a , temos:

Mas, tende ao infinito, assim:

Onde o sinal depende do valor de . Isso mostra que, realmente, há uma assíntota vertical em .

Prontinho, galera!

Essa questão era difícil, mas mantendo a calma e tentando aplicar os passos lógicos dá tudo certo 😊