Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei de Gauss – Simetrias

Ver Teoria
Exercício 601234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Usp - Física 3 – P1 2018.1 - 3

Considere uma casca esférica (não condutora) que está centrada na origem P 0 . Ela é uniformemente carregada com carga Q > 0 e possui raio R , cujo centro situa-se à uma distância R + d de um plano infinito, uniformemente carregado com uma densidade superficial σ > 0 , conforme mostrado na figura abaixo.

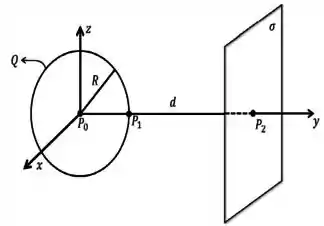
  1. Determine o vetor campo elétrico em todo o espaço devido à casca esférica.
  2. Determine o vetor campo elétrico em todo o espaço devido à carga na superfície plana.
  3. Determine o vetor campo elétrico resultante ao longo do eixo y > 0 .
  4. Calcule a diferença de potencial V 2 - V 0 entre os pontos P 2 e P 0 localizados na superfície plana e no centro da casca, respectivamente.

Passo 1

a) Usando a lei de Gauss, cuja superfície gaussiana é uma esfera de raio r , temos que

∮ S E → ⋅ d A → = E 4 π r 2 = Q i n t ϵ 0   ,

onde o vetor campo elétrico aponta na direção radial. Uma vez que Q i n t = 0 no interior da casca,   E → = 0 para r < R . Para r ≥ R , Q i n t = Q e, portanto,

E → = Q 4 π ϵ 0 r 2   r ^ ,

sendo que r a distância a partir do centro da esfera.

Passo 2

b) Usando a lei de Gauss, cuja superfície gaussiana é cilindro infinitesimal (veja figura abaixo), por simetria, o campo   E → é perpendicular ao plano e aponta na direção j ^ , se y > d + R e na direção - j ^ , se y < d + R .

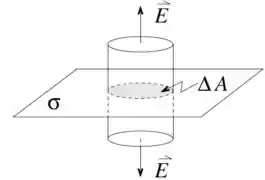
Além disso, ele só pode, em princípio, depender da distância até o plano. Portanto,

E → = - σ 2 ϵ 0   j ^ ,     p a r a   y < d + R ,  

e

E → = σ 2 ϵ 0   j ^ ,     p a r a   y > d + R   .

Passo 3

c) Utilizando o princípio da superposição, temos que, ao longo da direção y , o campo elétrico é dado por:

  • E → = - σ 2 ϵ 0 j ^   , para 0 < y < R
  • E → = - σ 2 ϵ 0 + Q 4 π ϵ 0 y 2 j ^   , para R < y < R + d , e
  • E → = σ 2 ϵ 0 + Q 4 π ϵ 0 y 2 j ^ ,   para R + d < y < ∞ .

    • Passo 4

    d) A partir da expressão

    V 2 - V 0 = - ∫ P 0 P 2 E → ⋅ d y →   ,

    obtemos que

    V 2 - V 0 = ∫ 0 R σ 2 ϵ 0   d y + ∫ R R + d σ 2 ϵ 0 - Q 4 π ϵ 0 y 2 d y   .

    Resolvendo essas integrais, obtemos que

    V 2 - V 0 = σ 2 ϵ 0 R + d + Q 4 π ϵ 0 1 R + d - 1 R   .

    Resposta

  1. E → = Q 4 π ϵ 0 r 2   r ^   ;
  2. E → = - σ 2 ϵ 0   j ^ ,     p a r a   y < d + R     ;     E → = σ 2 ϵ 0   j ^ ,     p a r a   y > d + R   ;
  4. E → = - σ 2 ϵ 0 j ^   , para 0 < y < R
  5. E → = - σ 2 ϵ 0 + Q 4 π ϵ 0 y 2 j ^   , para R < y < R + d , e
  6. E → = σ 2 ϵ 0 + Q 4 π ϵ 0 y 2 j ^ ,   para R + d < y < ∞ .
  7. V 2 - V 0 = σ 2 ϵ 0 R + d + Q 4 π ϵ 0 1 R + d - 1 R     .

Resposta

Ei, a resposta está no passo a passo :)

Exercícios de Livros Relacionados

A Fig. 23-30 mostra uma superfície gaussiana com a forma de um cubo de 2,00 m de aresta, imersa em um campo elétrico dado porE → = 3,00 x + 4,00 i ^ + 6,00 j ^ + 7,00 k ^ N / C , com x em metros. Qual
Uma fina casca esférica não-condutora de raio R 1 tem carga total q 1 uniformemente distribuída em sua superfície. Uma segunda fina casca esférica não condutora e maior, de raio R 2 , coaxial com a pr
Uma esfera de raio R tem densidade volumétrica de carga ρ = B / r para rR , onde B é uma constante e ρ = 0 para rR . (a) Determine a carga total na esfera. (b) Determine as expressões par ao campo elé
Um cilindro sólido não condutor infinitamente longo de raio a tem uma massa específica volumétrico uniforme de ρ 0 . Mostre que o campo elétrico é dado pelas seguintes expressões: E R = ρ R / 2 ε 0 pa
Uma fina casca cilíndrica de comprimento 200m e raio 6,00c m tem uma densidade superificial uniforme de carga de 9,00n C / m 2 . (a) Qual é a carga total na casca? Determine o campo elétrico nas segui