Uma esfera condutora maciça de raio encontra-se carregada com uma carga total . Ela está envolvida por uma casca esférica isolante de raio interno e raio externo (), uniformemente carregada com uma densidade volumétrica de carga , como mostrado na figura abaixo. A esfera e a casca são concêntricas e o sistema se encontra em equilíbrio eletrostático.
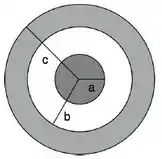
Utilizando a lei de Gauss, determine o vetor campo elétrico produzido pelo sistema em um ponto a uma distância r do centro da esfera. Considere todas as regiões distintas do espaço, dadas por
(i); (ii) ; (iii) ; e (iv) .
Justifique cuidadosamente todos os argumentos utilizados.
Passo 1
O enunciado fala pra gente que a esfera condutora está em equilíbrio eletrostático, a partir disso a gente consegue concluir que toda a carga dela está na superfície. Como a casca isolante está uniformemente carregada, concluímos também que o problema tem simetria esférica, ou seja, a distribuição de cargas na esfera condutora também vai ser uniforme :)
Vamos imaginar agora dois elementos de carga infinitesimal em posições polares opostas na esfera, porém, na mesma distância até o centro. As componentes de seus campos elétricos que forem perpendiculares à direção radial se cancelam, então, graças a essa simetria, o nosso campo elétrico vai ser apenas
sendo a distância até o centro da esfera.
Como a gente já sabe o formato e a expressão do campo, basta escolhermos uma superfície gaussiana e de raio concêntrica à esfera e à casca e calcularmos o fluxo de campo elétrico em para cada região que o enunciado pede.
Passo 2
Então vamo lá, o fluxo de campo elétrico na superfície gaussiana vai ser
Lembrando que o vetor normal a coincide com , temos que
Como o campo elétrico é constante em toda a superfície:
Ah! A área da superfície de uma esfera é
Ta, mas e agora?
Pela Lei de Gauss, sabemos que o fluxo elétrico deve ser igual a . é a carga dentro da superfície , mas ela vai depender do valor de , então vamos analisar cada uma das situações de dadas pelo enunciado ok?
Passo 3
i)
Quando , a superfície gaussiana está totalmente interna à esfera condutora.
Lembra que no passo 1 a gente concluiu que toda a carga está na superfície da esfera, e não dentro dela? Então, nesse caso a gente sabe que vai ser , logo:
ii)
Nessa região, a superfície gaussiana está entre a esfera e a casca, então a carga dentro dela vai ser apenas a carga na superfície da esfera, ou seja, .
iii)
Agora a superfície da gaussiana está dentro da casca, então a carga total dentro dela vai ser a carga na superfície da esfera + uma parte da carga da casca.
Como a casca está uniformemente carregada e tem uma densidade volumétrica de carga , a sua carga vai ser assim
Onde é o volume da casca que está no interior da superfície gaussiana. Logo, vai ser escrita como
A carga total dentro da gaussiana, então, vai ser
Então, podemos escrever que
iv)
Agora a superfície gaussiana engloba tanto a esfera quanto a casca, então a carga dentro dela vai ser a soma da carga da esfera com a carga total da casca:
Então: