Uma placa isolante, infinita e de espessura está posicionada de forma que seu plano médio coincida com o plano , como mostrado na figura abaixo.
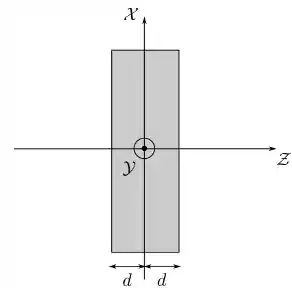
Ela está carregada com uma densidade volumétrica de carga constante e positiva.
Utilizando a lei de Gauss, determine o campo elétrico (módulo, direção e sentido) na região externa à placa, ou seja, .
Utilizando a lei de Gauss, determine o campo elétrico (módulo, direção e sentido) na região interna à placa, ou seja, .
Mostre que o resultado do item é equivalente ao campo produzido por um plano infinito uniformemente carregado com uma densidade superficial de carga . Expresse o valor de em termos dos parâmetros do problema e interprete o resultado.
Passo 1
Utilizando a lei de Gauss, determine o campo elétrico (módulo, direção e sentido) na região externa à placa, ou seja, .
Opa! Já que o problema mandou, vamos utilizar a Lei de Gauss aqui, que é dada por:
Quando estamos falando de placas infinitas carregadas, o campo elétrico é sempre perpendicular à superfície da placa. Neste caso, como a densidade volumétrica de carga é positiva, as linhas de campo elétrico vão sair da placa.
Então, pra esse caso, nós escolhemos como gaussiana uma superfície como um cilindro, se liga:
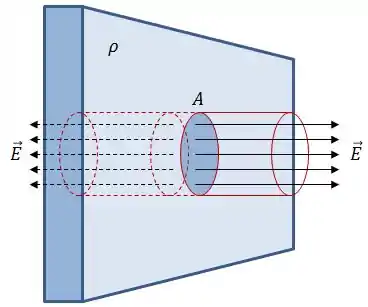
Obs.: Na verdade, vamos ver adiante que poderíamos escolher um cilindro ou um prisma como um paralelepípedo, ou algo do tipo, porque no final das contas essa área não vai importar, mas vou te lembrar disso mais à frente.
Fazendo isso em todos os pontos das tampas do nosso cilindro o módulo do campo elétrico será constante e os vetores e serão paralelos. Logo, podemos escrever a Lei de Gauss da seguinte forma:
Obs.: Consideramos uma área igual a porque o vetor campo elétrico está atravessando as duas faces da nossa gaussiana cilíndrica, cada uma com área .
Agora, a única coisa que temos que fazer é determinar, para cada caso, a carga no interior da gaussiana.
Passo 2
Para a nossa gaussiana estará englobando toda a espessura da placa:
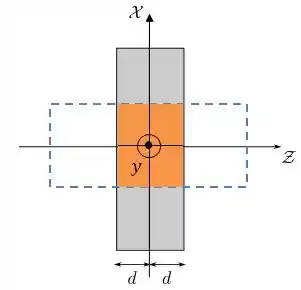
Assim, sabendo que a densidade volumétrica de carga é constante, a carga será dada por:
Onde corresponde ao volume da área em laranja. Dessa forma:
Substituindo na expressão do campo elétrico, teremos:
Pelos nossos argumentos de simetria, discutimos que o campo tem que apontar na direção positiva de para . Assim
Passo 3
Utilizando a lei de Gauss, determine o campo elétrico (módulo, direção e sentido) na região interna à placa, ou seja, .
Nesse caso, a nossa gaussiana irá englobar apenas parte da espessura da placa, como mostrado abaixo:
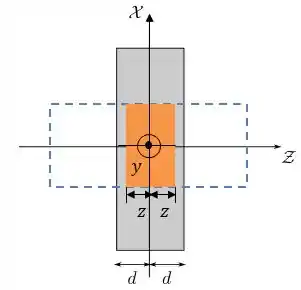
Nesse caso, a carga será dada por:
Onde é o volume da área laranja. Dessa forma:
Substituindo na expressão do campo elétrico, teremos:
De novo pelos nossos argumentos de simetria, o campo tem que apontar na direção positiva de para . Assim
Passo 4
Mostre que o resultado do item é equivalente ao campo produzido por um plano infinito uniformemente carregado com uma densidade superficial de carga . Expresse o valor de em termos dos parâmetros do problema e interprete o resultado.
A ideia aqui é a mesma que utilizamos na letra :
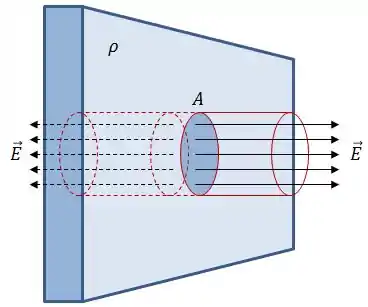
Aplicando a Lei de Gauss, novamente teríamos:
A diferença é que, agora, a carga está distribuída na superfície da placa, e não no seu volume. Sendo assim, vamos trabalhar com o conceito de densidade superficial de carga (que nesse casso é uniforme):
Onde corresponde à área englobada pela gaussiana. Substituindo na expressão do campo elétrico, teremos:
Se igualarmos essa expressão à expressão que encontramos na letra , teremos:
Passo 5
E agora temos que interpretar esse resultado! Pensa só: nós igualamos o campo de uma distribuição volumétricas de cargas com o campo de um plano infinito com densidade superficial de cargas e relacionamos e no passo anterior.
Se pegarmos a relação do passo anterior e multiplicarmos pela área da placa vamos ter
Sendo que é o volume da placa, assim
O lado direito da equação é a carga total da nossa placa! Já o lado esquerdo podemos escrever como
Ou seja, se pegássemos a nossa placa e olhássemos ela beeeem de longe, nós não diferenciaríamos ela da outra placa com densidade superficial de cargas da equação acima! Então no limite onde a espessura da placa é desprezível a gente pode pensar que a nossa placa original é um plano infinito com densidade superficial de carga .
Beleuza?
Resposta
Interpretação no passo 5