Uma partícula com carga foi depositada bem no centro da cavidade de uma casca esférica condutora de raio interno e raio externo . O gráfico ao lado da figura mostra o fluxo através de uma esfera gaussiana com centro na partícula em função do raio da esfera.
(Considere ou .)
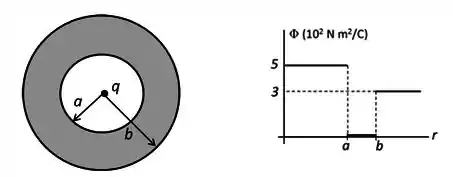
Determine a carga da partícula central e a carga líquida presente na casca condutora.
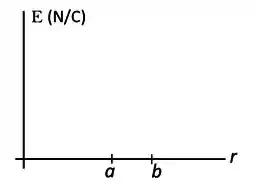
Considere agora que e . Encontre a dependência do campo elétrico como função de , para as três regiões: , e . Depois , copie na folha de respostas o par de eixos a seguir e esboce nele a função encontrada, calculando os valores importantes e explicitando no gráfico.
Remove-se a partícula e a cavidade é preenchida com um material isolante. A carga no isolante apresenta simetria esférica e densidade volumétrica dada pela função , onde é uma constante. Esta distribuição de carga provoca um campo elétrico radial e de módulo constante e igual a dentro da cavidade. Calcule o valor da constante com sua respectiva unidade SI.
Passo 1
Vamos primeiro determinar a carga que está no centro da cavidade, para isso vamos utilizar a lei de Gauss, que nos diz:
Para uma gaussiana esférica de raio menor que , temos:
Para determinar a carga líquida da casca esférica, utilizaremos uma gaussiana esférica de raio superior a :
Nossa carga interna será a carga depositada no centro da cavidade somada a carga líquida da casca esférica:
Substituindo, temos:
vambora pro próximo item!
Passo 2
Vamos agora determinar o campo para as três regiões, para isso usaremos..tchan tchan tchan tchaaannnnn...a lei de Gauss, só que daquele jeitinho maroto, se liga!
Lembrando que o campo será radial e constante, podemos calcular assim:
Em :
Onde é a área da gaussiana esférica, perceba que só podemos fazer isso pois o campo é constante e porque o vetor área será sempre paralelo ao campo! Substituindo os valores, temos:
Como temos que construir o gráfico, é valido determinar o valor do campo para :
Em :
Nesse intervalo estamos dentro da casca esférica, e sabemos que o campo elétrico dentro de um condutor é....zero!!
Em :
Lembre-se que é a soma de todas as cargas internas, ou seja, de e . Substituindo os valores, temos:
Por conta do gráfico vamos determinar o valor do campo em :
O gráfico deve ficar assim:
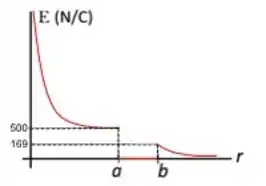
Eu sei...eu sei!! Ficou feio...mas dá para entender! =]
Passo 3
Para determinar o valor da constante vamos novamente utilizar a Lei de Gauss, temos então:
Por conta da simetria esférica, temos que o vetor área é sempre paralelo ao vetor campo, além de sabermos que este é constante:
Beleza, vamos agora determinar quanto vale a carga interna:
Vamos substituir isso na fórmula da lei de Gauss:
Simplificando, temos:
Substituindo os valores, temos;
Resposta