Uma esfera metálica maciça de raio é concentricamente circundada por uma casca esférica metálica com raios interno e externo , como mostrado na figura abaixo.
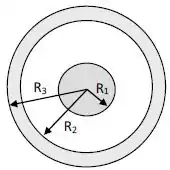
O fluxo elétrico através de uma superfície esférica gaussiana de raio vale . Sabendo que a esfera maciça possui uma carga e considerando que e :
Calcule, utilizando a Lei de Gauss, a distribuição das cargas nas superfícies externa e interna da casca esférica. Qual é o valor da carga líquida da casca? Justifique as afirmações e os cálculos.
Calcule o valor do módulo do campo elétrico na superfície da esfera maciça e na superfície externa da casca.
Considere agora que a casca esférica metálica é substituída por uma casca esférica isolante com e (desenho abaixo). A casca isolante é carregada uniformemente com uma carga igual ao valor da carga líquida da casca metálica anterior.
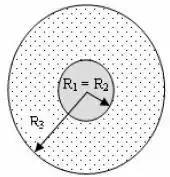
Calcule o valor do fluxo elétrico através de uma superfície gaussiana esférica de raio .
Passo 1
Calcule, utilizando a Lei de Gauss, a distribuição das cargas nas superfícies externa e interna da casca esférica. Qual é o valor da carga líquida da casca? Justifique as afirmações e os cálculos.
Tudo muito bonito... mas antes de começarmos a pensar nas distribuições de cargas nas superfícies externa e interna da casca esférica, primeiro precisamos descobrir a carga total da casca esférica , concorda?
O enunciado nos disse que, para , o fluxo elétrico . Além disso, , e .
Beleza! Quando o cara fala de fluxo elétrico no enunciado, no fundo, ele está pedindo pra usarmos a Lei de Gauss:
Aqui, com os dados que temos, a fórmula que temos que usar é:
No caso em que a gaussiana é uma esfera de raio , na região englobada pela gaussiana, estão tanto a esfera como a casca condutora. Sendo assim:
Portanto:
Substituindo os valores:
Agora sim!
Agora podemos calcular a carga nas superfícies interna e externa da casca esférica.
Passo 2
- Superfície interna:
- Superfície externa:
- Superfície da esfera:
- Superfície externa da casca esférica:
Se tivéssemos apenas a casca esférica carregada com carga , toda essa carga se encontraria na superfície externa da casca, de forma que a superfície interna teria carga nula.
Mas assim que colocamos a esfera com carga no interior da casca esférica, uma determinada quantidade de carga negativa será atraída pela esfera, assim como uma determinada quantidade de carga positiva vai ser repelida.
No equilíbrio eletrostático, a carga atraída para a superfície interna deve ser igual, em módulo, à carga da esfera , mas com o sinal oposto:
Beleza! Já sabemos que uma determinada quantidade de carga vai ser atraída para a superfície interna, e outra será repelida para superfície externa. Independente disso, a carga total da casca deve permanecer constante, logo:
Logo:
Passo 3
Calcule o valor do módulo do campo elétrico na superfície da esfera maciça e na superfície externa da casca.
Novamente vamos ter que usar a Lei de Gauss:
Como queremos calcular o módulo do campo elétrico, por causa da geometria esférica, podemos simplificar a Lei de Gauss:
Onde é a área da nossa gaussiana esférica:
Onde .
Opa! Então o nosso único trabalho aqui é determinar e para cada caso:
Logo:
Logo:
Passo 3
Calcule o valor do fluxo elétrico através de uma superfície gaussiana esférica de raio .
Opa! Já que temos que calcular o fluxo elétrico, vamos voltar a usar a Lei de Gauss:
Esse raio da nova gaussiana vale:
O problema aqui é calcular a carga interna . A gaussiana engloba a esfera e parte da casca isolante. Então temos que definir a quantidade de carga referente à porção da casca esférica englobada pela gaussiana.
Como a carga está uniformemente distribuída na casca, temos apenas que usar uma regra de 3 pra resolver a nossa vida:
Portanto:
Finalmente, agora é só calcular o fluxo elétrico:
Resposta