Uma esfera maciça isolante de raio está positivamente carregada. A densidade de carga volumétrica uniforme é dada por . O campo elétrico dentro da esfera vale:
- , apontando radialmente para fora com relação ao centro da esfera.
- , apontando radialmente para dentro com relação ao centro da esfera.
- , apontando radialmente para fora com relação ao centro da esfera.
- , apontando radialmente para dentro com relação ao centro da esfera.
- , apontando radialmente para fora com relação ao centro da esfera
Passo 1
Precisamos calcular aqui o campo elétrico na região . Para isso, vamos usar a gaussiana esférica mostrada na figura abaixo.
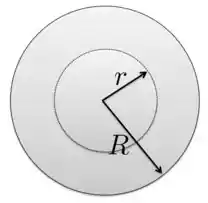
O primeiro passo aqui é notar que o campo elétrico tem simetria esférica, ou seja, a gente pode girar a esfera em torno de qualquer reta que passa pelo centro da esfera que teremos como resultado a mesma distribuição de cargas. Isso nos garante que o campo elétrico tem as seguintes características:
- O campo elétrico só tem componente radial: ;
- tem o mesmo valor nos pontos sobre a gaussiana;
- é paralelo a em todos os pontos da superfície gaussiana, como está na figura acima;
Com isso, podemos escrever o fluxo elétrico como:
em que a integral dá a área da superfície da gaussiana esférica.
Passo 2
Agora que já vimos o lado direito da lei de Gauss, vamos ver como fica a carga dentro da superfície gaussiana. O problema fala que a distribuição de cargas é uniforme. Isso significa que a densidade de cargas é a mesma em todos os pontos do interior da esfera carregada. Portanto, a densidade de cargas também é dentro da esfera gaussiana de raio .
Com isso, temos o seguinte:
Colocando essa expressão junto com aquela do Passo 1, temos:
Simplificando essa expressão, obtemos que o vetor campo elétrico dentro da esfera é
Como a carga da esfera é positiva, ou seja, , o campo elétrico é radial e aponta para fora se afastando do centro da esfera.
Resposta
Letra a.