Duas placas grandes, planas e orientadas horizontalmente são paralelas entre si, a uma distância uma da outra. A meio caminho entre as duas placas, o campo elétrico resultante tem magnitude . Se a separação das placas é reduzida para , qual é a magnitude do campo elétrico a meio caminho entre as placas?
(a)
(b)
(c)
(d)
(e)
Passo 1
Primeiramente, vamos relembrar o que é um plano infinito carregado.
Considere um plano com densidade superficial de cargas cujas dimensões são tais que é possível considerá-lo infinito. O campo elétrico devido ao plano é perpendicular ao plano. Veja a figura abaixo.
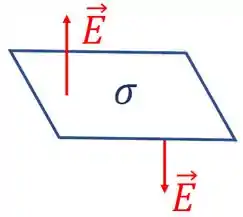
Na figura, , pois as linhas de campo saem do plano.
Podemos determinar o módulo do campo elétrico utilizando a lei de Gauss.
Esta lei diz que o fluxo de um campo elétrico por uma superfície fechada genérica é dada por
Na equação anterior, é a carga elétrica líquida dentro da superfície .
A ideia é utilizar uma superfície gaussiana adequada para determinar o módulo do campo elétrico. Faremos isso no próximo passo.
Passo 2
Vamos tomar a superfície gaussiana como um cilindro. Veja na imagem abaixo.
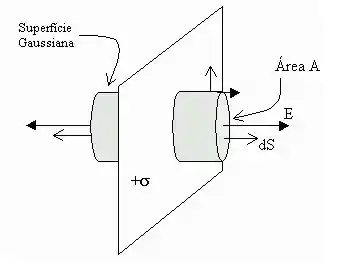
Assim, pela lei de Gauss, temos que
Na superfície gaussiana, o campo elétrico é perpendicular a lateral do cilindro e paralelo nas tampas. Deste modo, temos que
com a área da tampa (de cima ou de baixo).
Assim, temos que
Vamos determinar a carga dentro da superfície gaussiana. Sabemos que a densidade superficial de carga do plano é . Deste modo, temos imediatamente que
Desta forma, finalmente temos que
Note que o módulo do campo elétrico é constante! Isso significa o campo elétrico tem a mesma intensidade em todos os pontos sobre o plano!
Vamos para o próximo passo para continuarmos nossa análise.
Passo 3
O enunciado diz que existem duas placas grandes, planas e orientadas horizontalmente, que são paralelas entre si e estão a uma distância uma da outra. Assim, vamos supor que as placas são planos infinitos carregados e que uma das placas possua uma densidade de carga e a outra . Veja a figura.
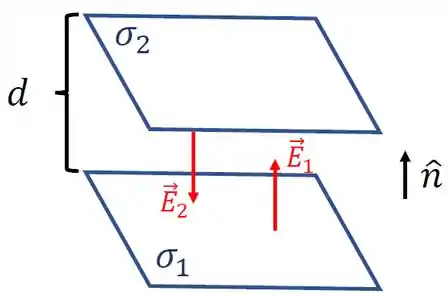
Na figura anterior, é um vetor unitário perpendicular às placas.
Utilizando o resultado do passo anterior, sabemos que o campo elétrico gerado por cada placa será
Assim, o campo elétrico resultante entre as placas é dado por
Note que o campo elétrico resultante é constante, isto é, não depende da posição em que se é medido.
Continuando, o enunciado define como como a magnitude do campo elétrico resultante a meia distância entre as placas. Como o campo elétrico resultante é constante, temos imediatamente que
Note que também não depende da distância entre as placas. Isso será bem importante!!
Posteriormente, o enunciado diz que a distância entre as placas é reduzida pela metade e pergunta o que ocorre com .
Como não depende da distância entre as placas, então se mantem INALTERADO!
Assim, analisando as alternativas do exercício, vemos que a alternativa correta é a letra .