Uma pequena esfera oca condutora, com raio interno e externo , é concêntrica com uma grande esfera oca condutora, com raio interno e raio externo , conforme a figura abaixo. A carga total sobre a esfera oca interna é igual à e a carga total sobre a esfera oca externa é igual à . Determine o módulo, direção e sentido do campo elétrico em função da distância ao centro comum para as regiões:
E qual a carga total sobre (i) a superfície interna da esfera oca pequena; (ii) a superfície externa da esfera oca pequena; (iii) a superfície interna da esfera oca grande; (iv) a superfície externa da esfera oca grande?
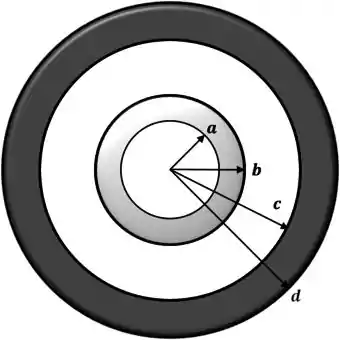
Passo 1
Questão clássica da Lei de Gauss. Mais uma vez vou explicar como você faria na prova pra não perder tempo nem pontos. São cinco regiões, só que nós vamos construir um argumento formal para resolver apenas uma, pois é isso que o examinador quer. Para as outras quatro, nós vamos dizer “...analogamente ao argumento da primeira região...” e vamos apenas aplicar a fórmula:
Partiu então? A sua resolução começaria, necessariamente, assim:
Enunciando a Lei de Gauss...
Pela simetria esférica do problema, escolhemos uma superfície esférica de raio arbitrário para ser nossa Gaussiana . Dessa forma, os vetores normais são paralelos ao campo em todos os pontos de , do que segue o fato:
Passo 2
Além disso, pela configuração do campo, temos que o seu módulo é constante em toda , do que segue o fato:
Da última equação, segue que a integral de em toda é a área da Gaussiana. A área superficial de uma esfera é conhecida e é igual à:
Substituindo na Lei, temos:
Passo 3
Aplicando o resultado obtido para a região onde :
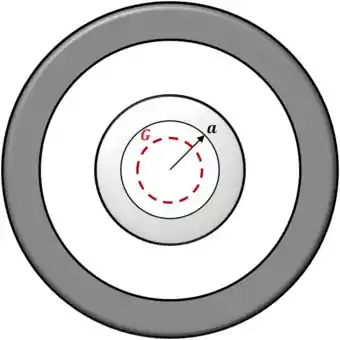
Temos que a nossa Gaussiana não envolve carga alguma, por estar em uma região de vácuo. Portanto:
Desde fato segue que:
Ou seja, nesta região o campo é o vetor nulo:
Passo 4
Analogamente ao raciocínio desenvolvido para a primeira região, aplicamos o resultado obtido para a região onde :
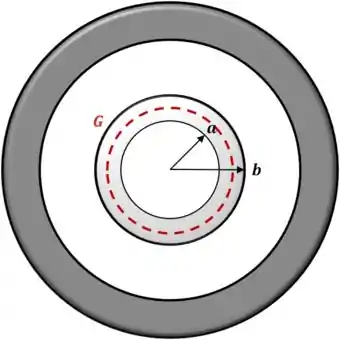
Neste caso estamos calculando o fluxo do campo elétrico na região maciça de um condutor. Não temos escolha senão dizer que o campo é nulo, dado que estamos no equilíbrio eletrostático. Portanto:
De onde segue que a carga interna à essa superfície Gaussiana é:
Passo 5
Mais uma vez, aplicando o mesmo raciocínio à região onde :
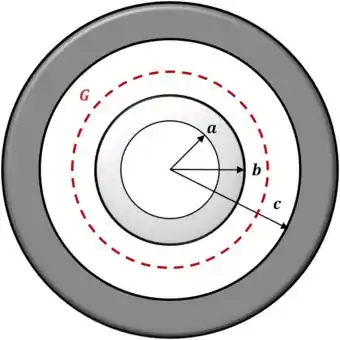
Neste caso a nossa Gaussiana envolve toda a esfera oca menor, portanto a carga interna à ela deve ser a carga total da esfera:
De onde segue que:
Ainda pelo argumento de simetria, a componente do campo deve ser radial. Portanto multiplicamos pelo vetor radial :
Passo 6
Você já deve estar ficando de saco cheio. Mas por outro lado, isto é muito próximo de uma questão de prova. Repare como nós vamos ganhando pontos com trabalho braçal apenas. Aplicando o raciocínio desenvolvido na primeira região para a região em que :
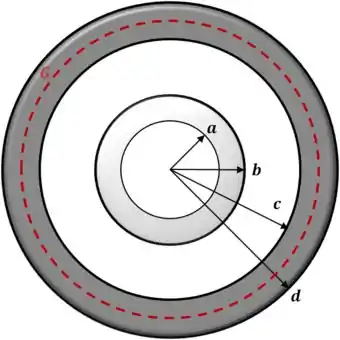
Temos que, por se tratar de uma região maciça de um condutor, não pode haver campo.
Segue que, pela Lei de Gauss, a carga interna à esta Gaussiana é zero:
Passo 7
Mais uma vez, pela mesma lógica, temos a região onde :
Segue então:
Neste caso, no entanto, temos que a carga interna à Gaussiana é tanto a carga da esfera maior quanto da menor, pois ambas são internas à . Portanto:
Podemos substituir:
E pelo argumento de simetria, temos que a componente do campo será radial:
Passo 8
Juntando tudo isto que observamos podemos descobrir as cargas nas superfícies. Do passo tiramos que a carga na superfície interna à esfera pequena é zero:
Do passo tiramos que a carga na superfície externa da esfera pequena é a sua carga total:
Já do passo 6, nós temos que a carga interna à Gaussiana deve ser zero, isto implica na carga da superfície interna da esfera grande ser o seguinte:
Só pra deixar bem claro, quando falamos de carga interna à Gaussiana, estamos falando da carga que fica interna ao seu volume. Aqui nesse contexto, temos superfícies internas e externas das esferas, que não são a mesma coisa. Qualquer coisa nos grite.
Seguindo... Como a carga total da esfera grande é , nós precisamos que esse valor seja a soma da carga na sua superfície externa e na sua interna. Portanto:
Logo:
E terminamos!