Uma corda de massa desprezível e inextensível está enrolada ao redor de um disco uniforme de raio e de massa e possui a outra extremidade fixada numa barra (conforme mostra a figura). O disco, liberado a partir do repouso, cai com a corda na posição vertical e mantém o seu eixo de rotação sempre na mesma direção. Dado: o momento de inercia de um disco de raio e de massa , segundo um eixo que passa pelo seu centro e perpendicular a sua superfície, é igual a .
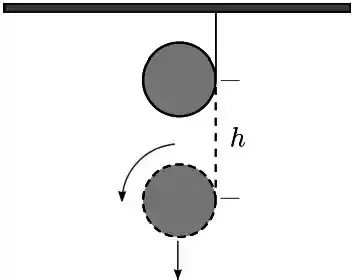
- Determine a aceleração do centro de massa do disco.
- Qual é o módulo da tensão na corda?
- Qual é a velocidade do centro de massa após o disco ter descido uma altura ?
- Qual é a razão entre as energias cinéticas de rotação e de translação , na mesma situação do item c)?
Passo 1
a)
As únicas forças que atuam no disco são a tração e o peso. Considerando que o disco rola no senti anti-horário, vamos ter para a rotação
Além disso a única força que gera torque é a tração já que ele roda pelo centro de massa.
O sentido do torque é anti-horário então temos a primeira equação
Lembrando que
E, para um disco
Finalmente resultando em
Passo 2
Para a translação, considerando que a aceleração do centro de massa tem módulo
Isso porque ele está caindo
No passo 1 achamos o valor da tração pela aceleração do centro de massa então
Passo 3
b)
agora que temos a aceleração do centro de massa a tração vai ser
Passo 4
c)
A energia mecânica se conserva já que não temos uma força dissipativas como o atrito.
Isso porque vamos considerar a altura que ele chega como zero, sendo a altura que ele está como .
Temos a energia cinética de rotação e a energia cinética de translação
Lembrando que
Vamos ter
O momento de inércia está ali em cima no passo 1
Passo 5
A energia cinética de translação vai ser
Tendo então
Passo 6
Igualando as energias
Passo 7
d)
Já encontramos cada uma dessas energias então