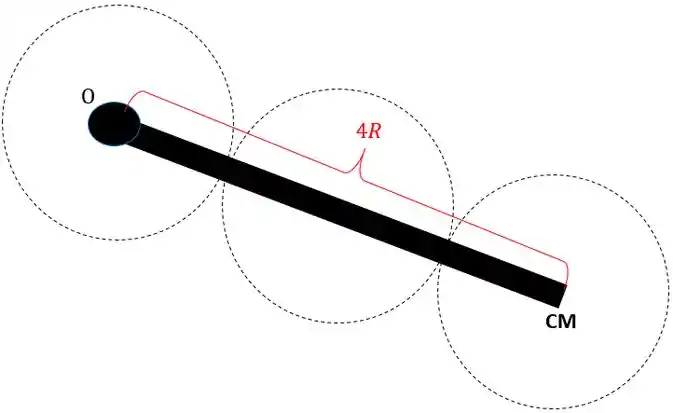
Um objeto é composto por uma haste de massa desprezível e comprimento ligada ao centro de três discos de massa e raio como ilustra a figura. Este objeto está no plano vertical pode girar livremente em torno do eixo . No instante indicado na figura, a haste encontra-se inclinada de em relação ao eixo . O objeto está em equilíbrio estático, devido à força que tem direção perpendicular à haste. Despreze atritos. A aceleração da gravidade é .
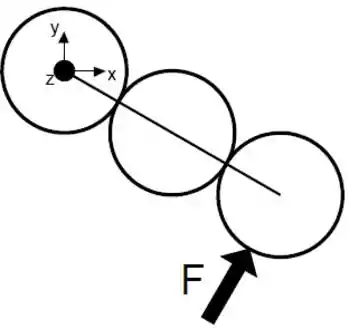
a) Calcule o torque produzido pela força e o torque produzido pela força da gravidade em termos dos dados do enunciado acima.
b) Suponha agora que , e . Em a força desaparece e o torque resultante é dado por . Calcule o módulo da aceleração angular para este instante e também para quando o objeto passar pela posição vertical.
Passo 1
a)
O torque da força é dado por:
está sendo aplicada na ponta da haste, a uma distância da origem. Portanto, sendo o módulo da força , temos
E pela regra da mão direita, o torque aponta na direção do vetor .
Ou seja,
Passo 2
Agora vai complicar um pouco, mas também nada de mais.
Queremos o torque realizado pela força da gravidade, e essa age no centro de massa CM do objeto, que fica bem no meio da haste.
E essa haste tem massa desprezível, então a massa total do objeto, concentrada no CM, é a soma das massas dos 3 discos, ou seja .
Então o torque realizado pela força da gravidade é:
Passo 3
Agora vamos ter que aplicar uma trigonometria pra achar esse ! Lembrando que ele é o vetor posição do ponto de aplicação da força em relação ao eixo de rotação. No caso, é o vetor posição do CM em relação à origem.
Já sabemos que o módulo de é :
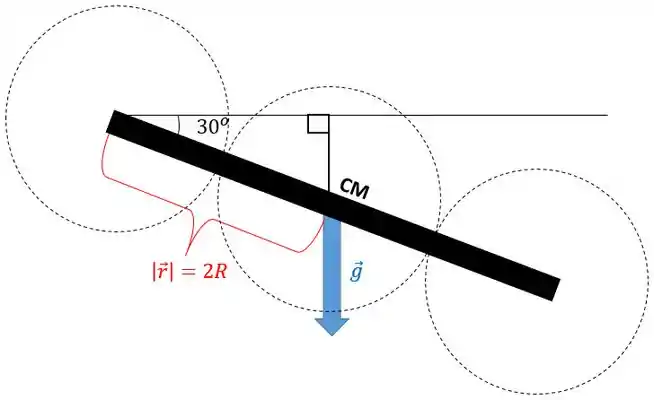
Passo 4
Mas o não tá na direção dos eixos e , então vai ser melhor decompor ele em e , o que dá:
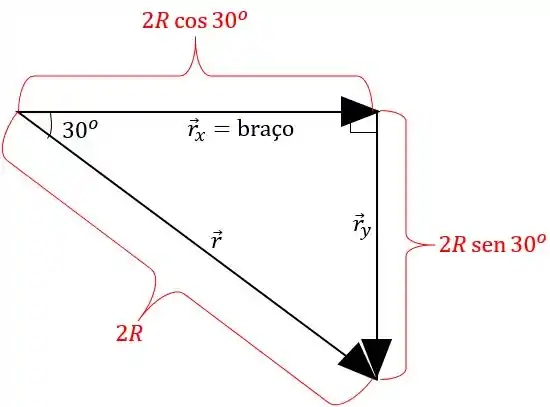
Passo 5
Temos
Repare que o braço da alavanca é a componente , a é paralela à força da gravidade , então ela não contribui à realização de torque. Então poderíamos usar como .
Enfim, se isso não te convenceu, ou se a gente só quiser verificar isso mesmo, podemos usar o todo mesmo:
Passo 6
E antes a gente viu que
Logo,
O produto vetorial é distributivo, e , então isso dá:
Mas então podemos cortar essa parte da direita! Que nem a gente previu antes! :)
Passo 7
Enfim, isso deu:
E então:
Passo 8
b)
A fórmula que relaciona torque resultante e aceleração angular é:
E ele disse que, no momento , o torque resultante é:
então basta a gente calcular o momento de inércia do objeto pra poder achar a aceleração angular em !
Passo 9
O objeto é composto por 3 discos de massa e raio e por uma haste, que por ter massa desprezível não contribui pro momento de inércia do objeto.
Então o momento de inércia do objeto é a soma dos momentos de inércia dos 3 discos! Separando eles em disco da esquerda, do meio e da direita, fica:
Isso em relação ao eixo de rotação, que é o eixo .
E o momento de inércia de cada disco em relação ao eixo passando pelo seu CM é
Então vamos achar o momento de inércia de cada disco! :D
Passo 10
No caso do disco mais à esquerda, o CM fica em cima do eixo de rotação, então seu momento de inércia em relação ao eixo é
Passo 11
Vamos pro disco do meio!
Vimos que o momento de inércia dele em relação ao eixo passando pelo seu CM é:
Mas a gente quer o momento de inércia em relação ao eixo , que está a uma distância do CM!
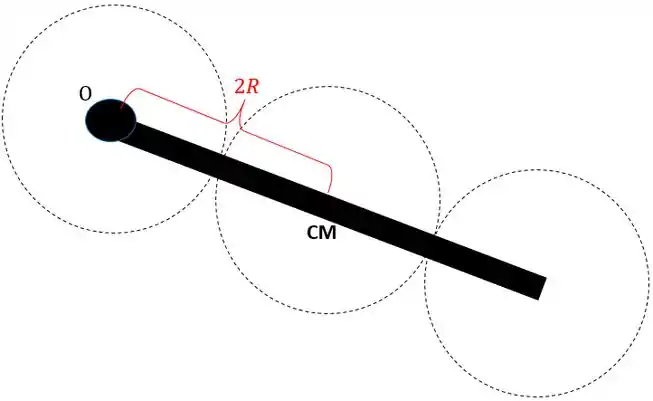
Então, aplicando o teorema dos eixos paralelos, temos:
Passo 12
Show, agora só falta o disco da direita!
A lógica é a mesma que pro disco do meio, a diferença é que a distância entre o eixo que passa pelo CM do disco e o eixo agora é .
 Ou seja,
Ou seja,
Passo 13
Ótimo! Então juntando tudo, obtemos:
Substituindo e , fica:
Passo 14
E isso tudo era pra gente jogar o valor do momento de inércia na fórmula:
Lembrando que ele deu , então:
Passo 15
Show, mas essa aceleração angular que a gente achou é no momento , que foi quando o torque resultante valia . E ele também pediu a aceleração angular quando o objeto passar pela posição vertical.
A única força atuando no objeto é a força da gravidade . Então o torque resultante é:
E novamente temos
Passo 16
Vamos dar uma olhada no que acontece quando o objeto está na vertical:
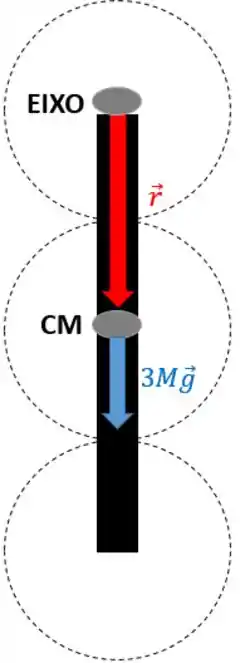
Os vetores e são paralelos, então o produto vetorial deles é nulo!
Portanto,
E como , a aceleração angular é nula:
Resposta
a)
b)
Em :
Quando o objeto passa na posição vertical: