O objeto ilustrado ao lado é composto de uma haste rígida de comprimento e de três partículas de massa . Inicialmente ele é mantido em repouso na posição horizontal através de um freio. No instante o freio é retirado e o objeto pode girar livremente em torno do eixo sob ação da força da gravidade. Despreze a massa da haste. Utilize para a aceleração da gravidade.

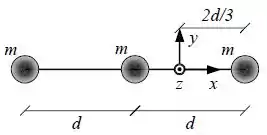
a) Mostre que o momento de inércia do objeto em torno do eixo é igual a .

b) Determine os torques resultantes e quando a haste ainda estiver na posição horizontal e depois de ter girado radianos.

c) Determine quando a haste ainda estiver na posição horizontal as acelerações lineares e das partículas nas extremidades esquerda e direita da haste.

d) Determine a energia cinética do objeto quando ele estiver passando pela posição vertical e sua aceleração angular nesta mesma posição.

No item (a), queremos mostrar que o momento de inércia em torno do eixo é:

Como a haste tem massa desprezível, o momento de inércia do sistema será apenas a soma dos momentos de inércia das partículas da esquerda, do meio e da direita:

O momento de inércia de uma partícula é dado pela multiplicação de sua massa com o quadrado da distância ao eixo de rotação:

Já sabemos a distância da partícula da direita ao eixo :

A distância da partícula do meio ao eixo será:

Enquanto a distância da partícula da esquerda ao eixo será:

Então, como todas as massas valem , temos que o momento de inércia desse sistema é:

Simplificando a fração, mostramos que o momento de inércia vale:

b) Determine os torques resultantes e quando a haste ainda estiver na posição horizontal e depois de ter girado radianos.

Como as três partículas tem a mesma massa, todas terão uma força de mesmo valor para baixo:

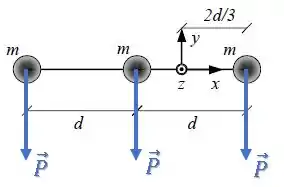
O torque de uma força é dado pelo produto vetorial do vetor distância com o vetor força :

O torque resultante será a soma dos torque da força peso de cada uma das três partículas:

Sendo o vetor , por exemplo, esse aqui:

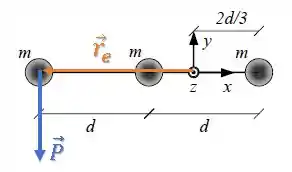
Como os vetores e são perpendiculares para as três partículas, os módulos (valor) dos torques serão os seguintes:

Mas precisamos ver também a direção e o sentido desses vetores.

Vamos usar a regra da mão direita:

Para as partículas da esquerda e do meio, nossos dedos apontam para a esquerda na direção de e fechamos nossos dedos para baixo na direção de . Então, nosso dedão está para “fora do papel” na direção :

Assim, os vetores e serão:

Enquanto isso, para a partícula da direita, nossos dedos apontam para a direita na direção de e fechamos nossos dedos para baixo na direção de . Então, nosso dedão está para “dentro do papel” na direção :

Logo, o vetor será:

Então o torque resultante será:

Substituindo os valores de e das distâncias , temos:

Nossa, chato pra caramba né?

Um monte de vetor e regra da mão direita pra lá e pra cá...

Tem um jeito mais fácil de fazer isso.

Como temos várias partículas, podemos considerar que todas elas estão concentradas na posição de centro de massa CM do sistema.

Aí, é só calcular o torque da força peso resultante nessa posição.

Beleza,tá vendo que as partículas estão espaçadas igualmente por ?

Então, o centro de massa do sistema vai cair exatamente em cima daquela partícula do meio.

Assim, podemos dizer que toda a massa do sistema está naquele ponto e calcular o torque resultante:

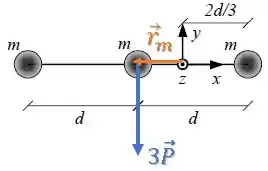
Então o torque resultante será:

Bem mais fácil, né?

Vamos calcular o torque resultante para uma rotação de :

Esse sistema vai girar no sentido horário, já que o torque está na direção .

Vamos calcular o torque para essa nova situação, utilizando novamente a ideia do centro de massa na partícula central:

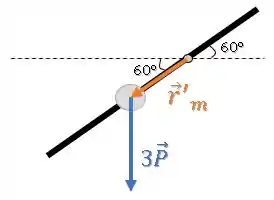
O torque resultante será:

Porém, agora esses vetores não são perpendiculares.

O jeito mais prático de resolver esse produto vetorial será decompor o distância e achar a distância perpendicular até a força:

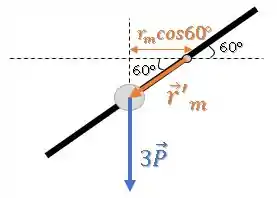
Então, o produto vetorial fica:

Substituindo os valores, temos:

c) Determine quando a haste ainda estiver na posição horizontal as acelerações lineares e das partículas nas extremidades esquerda e direita da haste.

Já achamos o torque resultante quando a barra está horizontal.

Então, podemos aplicar a segunda lei de Newton para rotação e achar a aceleração angular do conjunto:

Substituindo os valores, temos:

Já vimos que a aceleração angular está no sentido anti-horário. Nesse sistema de eixos, essa rotação apresenta direção , mesma direção e sentido do vetor torque

Podemos relacionar a aceleração angular com a aceleração linear por meio da distância da partícula ao eixo :

Então, a aceleração linear da partícula da esquerda será:

Enquanto a aceleração linear da partícula da direita será:

Já as direções serão:

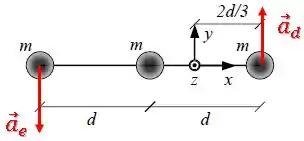
Então está em negativo equanto está em positivo:

d) Determine a energia cinética do objeto quando ele estiver passando pela posição vertical e sua aceleração angular nesta mesma posição.

Para encontrar podemos pensar na conservação da energia mecânica.

Mas, vamos usar de novo a posição do centro de massa como referência em vez que calcular a variação para cada partícula separadamente.

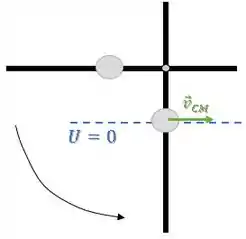
Inicialmente, temos apenas uma energia potencial gravitacional e nenhuma energia cinética, enquanto, no final, temos apenas energia cinética :

E qual foi a variação de altura?

Foi exatamente a distância da partícula central ao eixo :

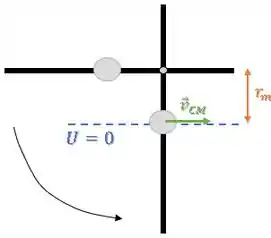
Então:

Já a aceleração angular nesse ponto depende do torque:

Porém, nesse instante, a força peso está vertical para baixo, assim como o vetor distância . Logo, o torque é nulo:

Assim, a aceleração angular também será nula: