UFMG, Sem Campus, Equações Diferenciais A, Listas de EDA - Profª Alejandra Russi - Lista 2 - Equações lineares, Bernoulli e separáveis, Questão 5.3
Resolva os problemas de valor inicial abaixo, indique o intervalo de validade da solução encontrada e esboce seu gráfico:
Passo 1
E aí gente, tudo beleza?
Nessa questão recebemos o seguinte problema de valor inicial (PVI):
E, sobre ele precisamos determinar a solução, o intervalo de validade dessa solução, como também o seu gráfico.
Ou seja, na prática precisamos resolver essa equação diferencial.
Bom, começando pelo intervalo de validade, pelo teorema da existência e unicidade precisamos verificar o intervalo em que:
e são contínuas.
Pra determinar a solução da EDO devemos pensar nas técnicas que dispomos para resolvê-la. A começar pela EDO separável, se conseguirmos colocar de um lado da igualdade tudo que depende de e do outro tudo que depende de , temos uma equação separável.
Excelente! Conseguimos!
Por fim, depois de encontrar a solução devemos esboçar o seu gráfico.
Vem com a gente que vai ficar tudo bem clarinho 😊
Passo 2
Pra começar vamos analisar o intervalo de validade. Temos a função:
E:
A única restrição em ambas as funções ocorre no denominador que não pode ser nulo. Ou seja:
Assim, o intervalo da solução, pelo teorema da existência e unicidade, e considerando também que a condição inicial foi dada em (e o intervalo de validade deve incluir a condição inicial):
Perfeito!
Passo 3
Agora vamos resolver a EDO em si. Vimos que:
Integrando em ambos os lados:
Temos:
E:
onde e são as constantes de integração. Igualando as duas integrais, podemos suprimir uma das constantes. Assim:
Daí, usando a condição inicial:
Vem que:
Logo:
Daí, vamos ter:
Perfeito! Conseguimos determinar .
Passo 4
Por fim, vamos desenhar o seu gráfico. Com auxílio dos recursos computacionais (como Geogebra, desmos e etc), devido à complexidade da função, temos o seguinte esboço:
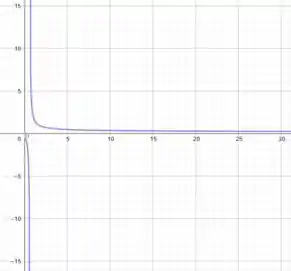
Agora sim galerinha, matamos a questão!!
Conseguiram entender bem? Responde Aí!
Resposta
Resposta no texto.